An implicit memory of errors limits human sensorimotor adaptation
- PMID: 33542527
- PMCID: PMC11910176
- DOI: 10.1038/s41562-020-01036-x
An implicit memory of errors limits human sensorimotor adaptation
Abstract
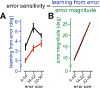
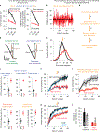
During extended motor adaptation, learning appears to saturate despite persistence of residual errors. This adaptation limit is not fixed but varies with perturbation variance; when variance is high, residual errors become larger. These changes in total adaptation could relate to either implicit or explicit learning systems. Here, we found that when adaptation relied solely on the explicit system, residual errors disappeared and learning was unaltered by perturbation variability. In contrast, when learning depended entirely, or in part, on implicit learning, residual errors reappeared. Total implicit adaptation decreased in the high-variance environment due to changes in error sensitivity, not in forgetting. These observations suggest a model in which the implicit system becomes more sensitive to errors when they occur in a consistent direction. Thus, residual errors in motor adaptation are at least in part caused by an implicit learning system that modulates its error sensitivity in response to the consistency of past errors.
© 2021. The Author(s), under exclusive licence to Springer Nature Limited.
Conflict of interest statement
Competing interests
The authors declare no competing interests.
Figures
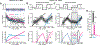




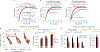
References
-
- Shadmehr R, Brandt J & Corkin S Time-dependent motor memory processes in amnesic subjects. J. Neurophysiol. 80, 1590–1597 (1998). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

