Quantifying the Stability of Coupled Genetic and Epigenetic Switches With Variational Methods

Abstract

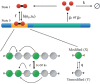
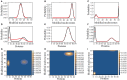
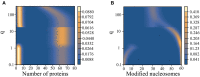
The Waddington landscape provides an intuitive metaphor to view development as a ball rolling down the hill, with distinct phenotypes as basins and differentiation pathways as valleys. Since, at a molecular level, cell differentiation arises from interactions among the genes, a mathematical definition for the Waddington landscape can, in principle, be obtained by studying the gene regulatory networks. For eukaryotes, gene regulation is inextricably and intimately linked to histone modifications. However, the impact of such modifications on both landscape topography and stability of attractor states is not fully understood. In this work, we introduced a minimal kinetic model for gene regulation that combines the impact of both histone modifications and transcription factors. We further developed an approximation scheme based on variational principles to solve the corresponding master equation in a second quantized framework. By analyzing the steady-state solutions at various parameter regimes, we found that histone modification kinetics can significantly alter the behavior of a genetic network, resulting in qualitative changes in gene expression profiles. The emerging epigenetic landscape captures the delicate interplay between transcription factors and histone modifications in driving cell-fate decisions.

Keywords: chromatin state; gene expression noise; gene network; minimum action; self-regulating gene.

Figure 1

Illustration of the kinetic model that couples the regulatory network of a self-activating gene with the reaction network of histone modifications. The gene is auto-regulatory as the protein produced by the gene (red circles) binds to the promoter region (yellow) with rate h and unbinds with rate f. Depending on whether the regulatory protein is bound (State 0) or unbound (State 1), the rate of protein production is g₀ or g₁. Proteins degrade with rate k. Conversions between modified (X) and unmodified (Y) nucleosomes can occur “randomly” (irrespective to the status of other nucleosomes) with a basal rate q. Nucleosome modifications can also occur more cooperatively with rate of z and s.

Figure 2

Comparison between the probability distributions obtained from the variational approach and from stochastic simulations. (A–C) Steady state probability distributions for the number of modified nucleosomes computed using the variational method (black solid line) and from stochastic simulations (red dots) for q = 100 (A), 10 (B), and 0.5 (C). (D–F) Steady state probability distributions for the number of protein molecules computed using the variational method (black solid line) and from stochastic simulations (red dots) for q = 100 (D), 10 (E), and 0.5 (F). (G–I) Steady state probability distributions as a function of both number of proteins and modified nucleosomes computed using the variational method for q = 100 (G), 10 (H), and 0.5 (I), showing two, one and two fixed points, respectively.

Figure 3

Dynamical trajectories determined from the variational approach agree well with stochastic simulations in favorable regimes. (A) Time evolution of the average number of modified nucleosomes computed using the variational method (black solid line) and stochastic simulations (red dots). (B) Time evolution of the average number of modified nucleosomes computed using the variational method (black solid line) and stochastic simulation (red dots). We used q = 10, M = 60, and set c₁p₁ = 0, c₀p₀ = 20, c₁t₁ = 0, c₁t₀ = 0.66 as the initial values when solving the deterministic equations (Equation 11).

Figure 4

Variation of the steady state probability distribution for the number of proteins (A) and modified nucleosomes (B) as a function of the noisy histone modification rate, q.