A compression strategy for particle mesh Ewald theory

Abstract

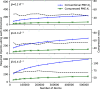
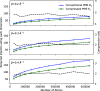
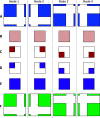
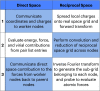
Particle Mesh Ewald (PME) has become a standard method for treating long-range electrostatics in molecular simulations. Although the method has inferior asymptotic computational complexity to its linear scaling competitors, it remains enormously popular due to its high efficiency, which stems from the use of fast Fourier transforms (FFTs). This use of FFTs provides great challenges for scaling the method up to massively parallel systems, in large part because of the need to transfer large amounts of data. In this work, we demonstrate that this data transfer volume can be greatly reduced as a natural consequence of the structure of the PME equations. We also suggest an alternative algorithm that supplants the FFT with a linear algebra approach, which further decreases communication costs at the expense of increased asymptotic computational complexity. This linear algebra based approach is demonstrated to have great potential for latency hiding by interleaving communication and computation steps of the short- and long-range electrostatic terms.

FIG. 1.

The grid dimension N₁(=N₂ = N₃) required in conventional PME to achieve a given force error and corresponding K₁(=K₂ = K₃) required in reciprocal space to achieve the same rms force error when using N₁ for the real space grid and a B-spline order of 4. The compression ratio (black dashed line) is defined as the ratio of the corresponding data volumes; see text for details.

FIG. 2.

The grid dimension N₁(=N₂ = N₃) required in conventional PME to achieve a given force error, and corresponding K₁(=K₂ = K₃) required in reciprocal space to achieve the same rms force error when using N₁ for the real space grid and a B-spline order of 8. The compression ratio (black dashed line) is defined as the ratio of the corresponding data volumes; see text for details.

FIG. 3.

Schematic 2D representation of the data held by each of the four nodes at each stage of the reciprocal space parallel communication scheme. (a) The real space potential grid, including halo regions. (b) After FFT of local data, to get each node’s partial contribution (indicated by the stripe pattern) to the structure factor. (c) After Reduce_scatter_block of the individual node contributions. (d) After convolution of local data with Eq. (4). (e) After Allgather communication of the convolved grid. (f) Inverse FFT to generate local potential grid, including halo regions.

FIG. 4.

Overview of the linear algebra based cPME algorithm detailed in the main text. Shaded boxes depict steps that are dominated by communication steps, and the complementary nature of the direct and reciprocal steps offers great potential for overlapping computation and communication.