Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design

Abstract

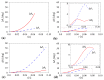
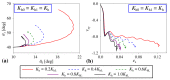
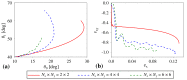
In this work, we use computer simulations (Molecular Dynamics) to analyse the behaviour of a specific auxetic hierarchical mechanical metamaterial composed of square-like elements. We show that, depending on the design of hinges connecting structural elements, the system can exhibit a controllable behaviour where different hierarchical levels can deform to the desired extent. We also show that the use of different hinges within the same structure can enhance the control over its deformation and mechanical properties, whose results can be applied to other mechanical metamaterials. In addition, we analyse the effect of the size of the system as well as the variation in the stiffness of its hinges on the range of the exhibited auxetic behaviour (negative Poisson's ratio). Finally, it is discussed that the concept presented in this work can be used amongst others in the design of highly efficient protective devices capable of adjusting their response to a specific application.

Keywords: Poisson’s ratio; auxetic; hierarchical; mechanical metamaterials.

Figure 1

The panels show (a) an example of the analyzed system corresponding to $N_x\times N_y=4\times 4$ where red arrows indicate constant external forces applied to the leftmost and rightmost points within the system and (b) a graphical representation of interactions responsible for rigidity of square elements (two-body bonded interactions) and hinging between them (three-body bonded interactions).

Figure 2

The panels show the behaviour of the system when hinges associated with level 0 and level 1 correspond to different values of a stiffness constant, namely: (a) $K_{h0}=K_{h1}=K_{hS}$ (all hinges are soft, $K_{hS}=1.23\times {10}^{-4}$ J deg${}^{-2}$), (b) $K_{h0}=K_{h1}=K_{hL}$ (all hinges are stiff, $K_{hL}=0.314$ J deg${}^{-2}$), (c) $K_{h0}=K_{hL}$ and $K_{h1}=K_{hS}$ (level 0 hinges are stiff and level 1 hinges are soft), and (d) $K{h}_0=K_{hS}$ and $K_{h1}=K_{hL}$ (level 0 hinges are soft and level 1 hinges are stiff). All of the results presented in this figure correspond to the system having level 1 structural blocks composed of $N_x\times N_y=4\times 4$ square units. In addition, $\mathrm{\Delta }{\theta }_i={\theta }_i\left(t\right)-{\theta }_i(t=0)$, where $i=0$ or $i=1$.

Figure 3

The panels show the evolution of the hierarchical system where: (a) $K_{h0}=K_{h1}=K_{hS}$ (all hinges are soft) and (b) $K_{h0}=K_{hL}$ and $K_{h1}=K_{hS}$ (level 0 hinges are stiff and level 1 hinges are soft).

Figure 4

The effect that the variation in the stiffness coefficient related to the hinges has on the behaviour of the structure. (a) the dependence of ${\theta }_1$ vs. ${\theta }_0$ during the deformation process and (b) the variation in the Poisson’s ratio for loading in the x-direction plotted against strain.

Figure 5

The effect of the variation in the number of squares constituting level 1 building blocks on the behaviour of the structure. These results were generated for structures where all off the hinges corresponded to the same stiffness coefficient equal to 0.2 $K_{hL}$. (a) the dependence of ${\theta }_1$ vs. ${\theta }_0$ during the deformation process and (b) the variation in the Poisson’s ratio for loading in the x-direction plotted against strain.