Adaptive social contact rates induce complex dynamics during epidemics
- PMID: 33566839
- PMCID: PMC7875423
- DOI: 10.1371/journal.pcbi.1008639
Adaptive social contact rates induce complex dynamics during epidemics
Abstract
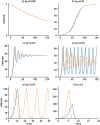
Epidemics may pose a significant dilemma for governments and individuals. The personal or public health consequences of inaction may be catastrophic; but the economic consequences of drastic response may likewise be catastrophic. In the face of these trade-offs, governments and individuals must therefore strike a balance between the economic and personal health costs of reducing social contacts and the public health costs of neglecting to do so. As risk of infection increases, potentially infectious contact between people is deliberately reduced either individually or by decree. This must be balanced against the social and economic costs of having fewer people in contact, and therefore active in the labor force or enrolled in school. Although the importance of adaptive social contact on epidemic outcomes has become increasingly recognized, the most important properties of coupled human-natural epidemic systems are still not well understood. We develop a theoretical model for adaptive, optimal control of the effective social contact rate using traditional epidemic modeling tools and a utility function with delayed information. This utility function trades off the population-wide contact rate with the expected cost and risk of increasing infections. Our analytical and computational analysis of this simple discrete-time deterministic strategic model reveals the existence of an endemic equilibrium, oscillatory dynamics around this equilibrium under some parametric conditions, and complex dynamic regimes that shift under small parameter perturbations. These results support the supposition that infectious disease dynamics under adaptive behavior change may have an indifference point, may produce oscillatory dynamics without other forcing, and constitute complex adaptive systems with associated dynamics. Implications for any epidemic in which adaptive behavior influences infectious disease dynamics include an expectation of fluctuations, for a considerable time, around a quasi-equilibrium that balances public health and economic priorities, that shows multiple peaks and surges in some scenarios, and that implies a high degree of uncertainty in mathematical projections.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


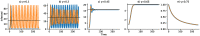
References
-
- Eichenbaum MS, Rebelo S, Trabandt M. The macroeconomics of epidemics National Bureau of Economic Research. 2020.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

