Mechanisms of Frank-Starling law of the heart and stretch activation in striated muscles may have a common molecular origin
- PMID: 33575955
- PMCID: PMC10905364
- DOI: 10.1007/s10974-020-09595-2
Mechanisms of Frank-Starling law of the heart and stretch activation in striated muscles may have a common molecular origin
Abstract
Vertebrate cardiac muscle generates progressively larger systolic force when the end diastolic chamber volume is increased, a property called the "Frank-Starling Law", or "length dependent activation (LDA)". In this mechanism a larger force develops when the sarcomere length (SL) increased, and the overlap between thick and thin filament decreases, indicating increased production of force per unit length of the overlap. To account for this phenomenon at the molecular level, we examined several hypotheses: as the muscle length is increased, (1) lattice spacing decreases, (2) Ca2+ sensitivity increases, (3) titin mediated rearrangement of myosin heads to facilitate actomyosin interaction, (4) increased SL activates cross-bridges (CBs) in the super relaxed state, (5) increased series stiffness at longer SL promotes larger elementary force/CB to account for LDA, and (6) stretch activation (SA) observed in insect muscles and LDA in vertebrate muscles may have similar mechanisms. SA is also known as delayed tension or oscillatory work, and universally observed among insect flight muscles, as well as in vertebrate skeletal and cardiac muscles. The sarcomere stiffness observed in relaxed muscles may significantly contributes to the mechanisms of LDA. In vertebrate striated muscles, the sarcomere stiffness is mainly caused by titin, a single filamentary protein spanning from Z-line to M-line and tightly associated with the myosin thick filament. In insect flight muscles, kettin connects Z-line and the thick filament to stabilize the sarcomere structure. In vertebrate cardiac muscles, titin plays a similar role, and may account for LDA and may constitute a molecular mechanism of Frank-Starling response.
Keywords: Delayed tension; Length dependent activation; Oscillatory work; Sarcomere length; Stiffness; Titin and kettin.
© 2021. The Author(s), under exclusive licence to Springer Nature Switzerland AG part of Springer Nature.
Conflict of interest statement
Figures
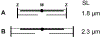




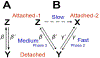

References
-
- Abbott RH. (1972). An interpretation of the effects of fiber length and calcium on the mechanical properties of insect flight muscle. Cold Spring Hbr Symp on Quant Biol 37, 647–654.
-
- Bers DM. (2002). Cardiac excitation-contraction coupling. Nature 415, 198–205. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

