Biochemical and phylogenetic networks-I: hypertrees and corona products

doi:10.1007/s10910-020-01194-3

. 2021;59(3):676-698.

doi: 10.1007/s10910-020-01194-3. Epub 2021 Feb 6.

Biochemical and phylogenetic networks-I: hypertrees and corona products

R Sundara Rajan¹, K Jagadeesh Kumar¹, A Arul Shantrinal¹, T M Rajalaxmi², Indra Rajasingh³, Krishnan Balasubramanian⁴

Affiliations

¹ Department of Mathematics, Hindustan Institute of Technology and Science, Chennai, 603 103 India.
² Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai, 603 110 India.
³ School of Advanced Sciences, Vellore Institute of Technology, Chennai, 600 127 India.
⁴ School of Molecular Sciences, Arizona State University, Tempe, AZ 85287-1604 USA.

PMID: 33583991
PMCID: PMC7867407
DOI: 10.1007/s10910-020-01194-3

Biochemical and phylogenetic networks-I: hypertrees and corona products

R Sundara Rajan et al. J Math Chem. 2021.

. 2021;59(3):676-698.

doi: 10.1007/s10910-020-01194-3. Epub 2021 Feb 6.

Authors

R Sundara Rajan¹, K Jagadeesh Kumar¹, A Arul Shantrinal¹, T M Rajalaxmi², Indra Rajasingh³, Krishnan Balasubramanian⁴

Affiliations

¹ Department of Mathematics, Hindustan Institute of Technology and Science, Chennai, 603 103 India.
² Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai, 603 110 India.
³ School of Advanced Sciences, Vellore Institute of Technology, Chennai, 600 127 India.
⁴ School of Molecular Sciences, Arizona State University, Tempe, AZ 85287-1604 USA.

PMID: 33583991
PMCID: PMC7867407
DOI: 10.1007/s10910-020-01194-3

Abstract

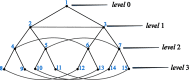
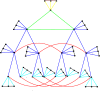
We have obtained graph-theoretically based topological indices for the characterization of certain graph theoretical networks of biochemical interest. We have derived certain distance, degree and eccentricity based topological indices for various k-level hypertrees and corona product of hypertrees. We have also pointed out errors in a previous study. The validity of our results is supported by computer codes for the respective indices. Several biochemical applications are pointed out.

Keywords: Biochemical networks; Corona product of graphs; Eccentricity-based topological indices; Mathematical modeling; Topological indices of hypertrees.

PubMed Disclaimer

Conflict of interest statement

Conflict of interestThe authors declare that there is no conflict of interests regarding the publication of this paper.

Figures

**Fig. 1**
Hypertree HT(3) of dimension 3

**Fig. 2**
The hypertree HT( $4$ ) with $n (v) = 14$

**Fig. 3**
The corona product HT(3) $⊙ P_{3}$ of hypertree HT(3) and path $P_{3}$

See this image and copyright information in PMC

Cited by

Biochemical and phylogenetic networks-II: X-trees and phylogenetic trees.
Rajan RS, Shantrinal AA, Kumar KJ, Rajalaxmi TM, Rajasingh I, Balasubramanian K. Rajan RS, et al. J Math Chem. 2021;59(3):699-718. doi: 10.1007/s10910-020-01195-2. Epub 2021 Feb 28. J Math Chem. 2021. PMID: 33678934 Free PMC article.

References

1. Ivorra B, Ramos AM, Ngom D. Be-CoDiS: a mathematical model to predict the risk of human diseases spread between countries. Validation and application to the 2014 ebola virus disease epidemic. Bull. Math. Biol. 2015;77(9):1668–1704. doi: 10.1007/s11538-015-0100-x. - DOI - PubMed
1. O. Diekmann, H. Heesterbeek, T. Britton, in Understanding Infectious Disease Dynamics. Princeton Series in Theoretical and Computational Biology, Princeton University Press, ISBN 978-1-4008-4562-0 (2013) http://www.jstor.org/stable/j.cttq9530
1. Bowman C, Gumel A, Driessche PV, Wu J, Zhu H. A mathematical model for assessing control strategies against West Nile virus. Bull. Math. Biol. 2005;67(5):1107–1133. doi: 10.1016/j.bulm.2005.01.002. - DOI - PubMed
1. Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020 doi: 10.1016/s1473-3099(20)30144-4. - DOI - PMC - PubMed
1. Roosa K, Lee Y, Luo R, Kirpich A, Rothenberg R, Hyman J. Real-time forecasts of the COVID-19 epidemic in china from February 5th to February 24th. Infect. Dis. Modell. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. - DOI - PMC - PubMed

LinkOut - more resources

Full Text Sources
- Europe PubMed Central
- PubMed Central
Other Literature Sources
- scite Smart Citations

[1] Ivorra B, Ramos AM, Ngom D. Be-CoDiS: a mathematical model to predict the risk of human diseases spread between countries. Validation and application to the 2014 ebola virus disease epidemic. Bull. Math. Biol. 2015;77(9):1668–1704. doi: 10.1007/s11538-015-0100-x. - DOI - PubMed

[2] Ivorra B, Ramos AM, Ngom D. Be-CoDiS: a mathematical model to predict the risk of human diseases spread between countries. Validation and application to the 2014 ebola virus disease epidemic. Bull. Math. Biol. 2015;77(9):1668–1704. doi: 10.1007/s11538-015-0100-x. - DOI - PubMed

[3] O. Diekmann, H. Heesterbeek, T. Britton, in Understanding Infectious Disease Dynamics. Princeton Series in Theoretical and Computational Biology, Princeton University Press, ISBN 978-1-4008-4562-0 (2013) http://www.jstor.org/stable/j.cttq9530

[4] O. Diekmann, H. Heesterbeek, T. Britton, in Understanding Infectious Disease Dynamics. Princeton Series in Theoretical and Computational Biology, Princeton University Press, ISBN 978-1-4008-4562-0 (2013) http://www.jstor.org/stable/j.cttq9530

[5] Bowman C, Gumel A, Driessche PV, Wu J, Zhu H. A mathematical model for assessing control strategies against West Nile virus. Bull. Math. Biol. 2005;67(5):1107–1133. doi: 10.1016/j.bulm.2005.01.002. - DOI - PubMed

[6] Bowman C, Gumel A, Driessche PV, Wu J, Zhu H. A mathematical model for assessing control strategies against West Nile virus. Bull. Math. Biol. 2005;67(5):1107–1133. doi: 10.1016/j.bulm.2005.01.002. - DOI - PubMed

[7] Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020 doi: 10.1016/s1473-3099(20)30144-4. - DOI - PMC - PubMed

[8] Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, Funk S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020 doi: 10.1016/s1473-3099(20)30144-4. - DOI - PMC - PubMed

[9] Roosa K, Lee Y, Luo R, Kirpich A, Rothenberg R, Hyman J. Real-time forecasts of the COVID-19 epidemic in china from February 5th to February 24th. Infect. Dis. Modell. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. - DOI - PMC - PubMed

[10] Roosa K, Lee Y, Luo R, Kirpich A, Rothenberg R, Hyman J. Real-time forecasts of the COVID-19 epidemic in china from February 5th to February 24th. Infect. Dis. Modell. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. - DOI - PMC - PubMed

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Biochemical and phylogenetic networks-I: hypertrees and corona products

Affiliations

Biochemical and phylogenetic networks-I: hypertrees and corona products

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

Similar articles

Cited by

References

LinkOut - more resources

Full Text Sources

Other Literature Sources