Estimation of Heterogeneous Restricted Mean Survival Time Using Random Forest

Abstract

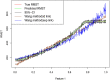
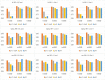
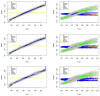
Estimation and prediction of heterogeneous restricted mean survival time (hRMST) is of great clinical importance, which can provide an easily interpretable and clinically meaningful summary of the survival function in the presence of censoring and individual covariates. The existing methods for the modeling of hRMST rely on proportional hazards or other parametric assumptions on the survival distribution. In this paper, we propose a random forest based estimation of hRMST for right-censored survival data with covariates and prove a central limit theorem for the resulting estimator. In addition, we present a computationally efficient construction for the confidence interval of hRMST. Our simulations show that the resulting confidence intervals have the correct coverage probability of the hRMST, and the random forest based estimate of hRMST has smaller prediction errors than the parametric models when the models are mis-specified. We apply the method to the ovarian cancer data set from The Cancer Genome Atlas (TCGA) project to predict hRMST and show an improved prediction performance over the existing methods. A software implementation, srf using R and C++, is available at https://github.com/lmy1019/SRF.

Keywords: estimating equation; high dimensional data; inference; non-parametric survival estimation; regression forest.

Figure 1

Training data are simulated from Equation (2), with n = 600 training points, dimension p = 20 and errors ϵ ~ N(0, 10²). Random forests are trained based using R package grf. Truth is shown as red curve, with green curve corresponding to the random forest predictions, and upper and lower bounds of the point-wise confidence intervals connected in the black lines. Brown curve and blue curve are based on the approaches of Wang and Schaubel (2018) with Identity and Exp link functions.

Figure 2

Simulation results of the coverage probability for Model 1 with three different link functions, sample size of n = 1, 000, 2, 000, 5, 000, and p = 2, 4, 6, 8. For each case, prediction coverage probability is calculated over the samples in the testing data set.

Figure 3

Simulation results of coverage probability for Model 2 with three different link functions, sample size of n = 1, 000, 2, 000, 10, 000, and p = 2, 4, 6, 8. For each case, prediction coverage probability is calculated over the samples in the testing data set.

Figure 4

Estimated vs. the true RMST for Model 1 (left) and Model 2 (right) with exponential link function and the number of covariates p = 5, 10, 20 (top–bottom). SRF, proposed random forest-bases estimator, and upper and lower bounds of the point-wise confidence intervals of the proposed random forest estimator are connected in the gray lines; Naive.km, estimate based on Kaplan–Meier estimator without adjusting for the covariates; Naive.Cox, Cox regression based estimator; Lu.id, method of Tian et al. (2014) with identity link; Lu.exp, method of Tian et al. (2014) with exponential link; Wang.id, method of Wang and Schaubel (2018) with identity link; Wang:exp, method of Wang and Schaubel (2018) with exponential link.

Figure 5

Performance of the proposed random forest estimator compared with other methods for L = 3, 4, 5. The left penal is the MAE across of 10-fold cross-validation. The right panel is the RMSE across of 10-fold cross-validation. SRF, proposed random forest estimator; Naive.km, estimate based on Kaplan–Meier estimator without adjusting for the covariates; Naive.Cox, Cox regression based estimator; Lu.id, method of Tian et al. (2014) with identity link; Lu.exp, method of Tian et al. (2014) with exponential link; Wang.id method of Wang and Schaubel (2018) with identity link; Wang:exp, method of Wang and Schaubel (2018) with exponential link.