Phosphate has dual roles in cross-bridge kinetics in rabbit psoas single myofibrils

Abstract

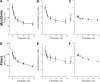
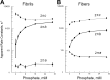
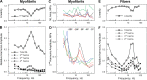
In this study, we aimed to study the role of inorganic phosphate (Pi) in the production of oscillatory work and cross-bridge (CB) kinetics of striated muscle. We applied small-amplitude sinusoidal length oscillations to rabbit psoas single myofibrils and muscle fibers, and the resulting force responses were analyzed during maximal Ca2+ activation (pCa 4.65) at 15°C. Three exponential processes, A, B, and C, were identified from the tension transients, which were studied as functions of Pi concentration ([Pi]). In myofibrils, we found that process C, corresponding to phase 2 of step analysis during isometric contraction, is almost a perfect single exponential function compared with skinned fibers, which exhibit distributed rate constants, as described previously. The [Pi] dependence of the apparent rate constants 2πb and 2πc, and that of isometric tension, was studied to characterize the force generation and Pi release steps in the CB cycle, as well as the inhibitory effect of Pi. In contrast to skinned fibers, Pi does not accumulate in the core of myofibrils, allowing sinusoidal analysis to be performed nearly at [Pi] = 0. Process B disappeared as [Pi] approached 0 mM in myofibrils, indicating the significance of the role of Pi rebinding to CBs in the production of oscillatory work (process B). Our results also suggest that Pi competitively inhibits ATP binding to CBs, with an inhibitory dissociation constant of ∼2.6 mM. Finally, we found that the sinusoidal waveform of tension is mostly distorted by second harmonics and that this distortion is closely correlated with production of oscillatory work, indicating that the mechanism of generating force is intrinsically nonlinear. A nonlinear force generation mechanism suggests that the length-dependent intrinsic rate constant is asymmetric upon stretch and release and that there may be a ratchet mechanism involved in the CB cycle.

Figure S1.

A typical force time course record from a fully Ca²⁺-activated myofibril experiment. (A) Length change (strain) with the amplitude of 0.2% L₀. Frequency (ν) is shown in Hz underneath each oscillation. (B) Tension and its transients as recorded simultaneously (the data pair were collected in every 0.5 ms). When oscillation was stopped, and if the tension is different before and after the oscillation at each frequency, a linear detrend was applied to the tension time course during the oscillation before deducing all kinetic parameters.

Figure S2.

A typical force time course record from skinned muscle fiber experiments. The standard activation was followed by rigor induction. The timing of the sinusoidal length changes (chg.) is schematically represented on the top of the figure. The amplitude (strain) was 0.125% L₀ for all frequencies. The thickness of the pen trace represents the orifice size of the pen and not the noise. The force record was photographically reproduced from the original pen trace.

Figure 1.

Active tension and stiffness. Active tension (in A and D), stiffness (elastic modulus, Y_∞, in B and E), and their ratio (tension/Y_∞ in C and F) are plotted against [P_i]. (A–C) Experiments with myofibrils (n = 9). (D–F) Experiments with muscle fibers (n = 10). Averages are shown with SEM (error bars).

Figure 2.

Nyquist plots of the complex modulus data of active preparations. These are plotted at four different [P_i] values (0, 2, 8, and 30 mM as indicated; these are amounts of P_i added to the saline). (A) Myofibrils (average of 12 preparations). (B) Muscle fibers (average of 10 preparations). A decrease of exponential process B (central circular loop, in part with negative viscous modulus) as [P_i] → 0 mM is seen in myofibrils (A) but not in fibers (B).

Figure 3.

Complex modulus (Mod) data Y(ν) of active muscle preparations. The data are plotted as a function of frequency at six [P_i] values: 0 mM (open squares), 2 mM (filled triangles), 4 mM (open diamonds), 8 mM (open circles), 16 mM (+), and 30 mM (×). (A and B) Experiments with myofibrils averaged for 12 preparations. (C and D) Experiments with muscle fibers averaged for 10 preparations. A and C show dynamic modulus (|Y(ν)|). B and D show phase shift (arg[Y(ν)]). Smooth curves indicate best-fit data to Eq. 4. The complex modulus Y(ν) was first calculated at each frequency (ν), then averaged for 10–12 preparations and plotted. This was essential because the data from individual preparations were noisy; to reduce the noise, averaging was performed.

Figure 4.

Effect of P_i on apparent rate constants. (A) Experiments with myofibrils averaged for 12 preparations. Y(f) was averaged first, then fitted to Eq. 4 to find the apparent rate constants 2πa, 2πb, and 2πc. (B) Experiments with muscle fibers for 10 preparations. The mean and SEM are shown, but most of the SEMs are smaller than the symbol size and cannot be seen.

Figure 5.

The effect of P_i on the apparent rate constant (Const) 2πc. (A) Averaged myofibril data (n = 14) fitted to Eq. 12 with I = [P_i]. (B) Averaged muscle fiber data (n = 10). These are the same data as those shown in Fig. 4 in the logarithmic scale.

Scheme 1.

CB scheme surrounding ATP binding steps. A, actin; M, myosin; I, inhibitor (competitive); X₂, [AM.ATP].

Figure 6.

The effect of P_i on exponential process B in myofibrils, averaged for 14 preparations and plotted with SEM. (A) Apparent rate constant (Const) 2πb (filled circles). The continuous curve is the best fit of the data to Eq. 13. (B) Magnitude B (filled squares). Averaged points are connected by straight lines. Small filled triangles in A indicate the peak (Fig. 7 D) position (ν_p) of the second harmonic amplitude; 2πν_p is entered here. Small filled triangles in B indicate the second harmonic amplitude (Fig. 7 D) at the peak position with baseline (0.06) subtraction and appropriate scaling (98×).

Scheme 2.

CB scheme surrounding the force generation and P_i release steps. This scheme describes two types of work: oscillatory work and linear work. X₄, X₅, and X₆ represent the concentration of species shown above, such as X₄ = [AM⋅ADP⋅P_i], X₅ = [AM*⋅ADP⋅P_i], and X₆ = [AM*⋅ADP]. J is the flux, defined by J₄ = k₄X₄, J₅ = k₋₄X₅, J₆ = J_{4 −} J₅ = ATP hydrolysis rate. Force generation occurs in step 4 and before P_i is released in step 5. Step 6 is the rate-limiting step and can be characterized by the ATPase rate. The essence of this scheme is based on three states (X₄, X₅, and X₆) and three kinetic constants (k₄, k₋₄, and K₅), which can be measured with sinusoidal analysis combined with the P_i effect (Kawai and Halvorson, 1991). This scheme is also consistent with that measured by caged-P_i experiments (Dantzig et al., 1992) and pressure-release experiments (Fortune et al., 1991).

Figure 7.

Harmonic amplitudes. (A, B, E, and F) Relative amplitudes of harmonic (harmo) components in force (Eq. 6) as functions of frequency in the 8 mM P_i solution. (A and E) Linearity (Lin; Eq. 7). (B and F) Nonlinearity (NL; Eq. 10) and relative amplitude of harmonic components RHA_k(ν) (k = 2, 3, 4; Eq. 6). (C) Total nonlinear amplitude (NLCM; Eq. 9) at five [P_i] values as keyed at the top of D. (D) Amplitude of second harmonic component of the complex modulus (|Y₂| in Eq. 3) at five [P_i] values. A–D show the results of the myofibril study as averaged data (n = 14). E and F show the results of the muscle fiber study (n = 10).