Estimating the cumulative incidence of SARS-CoV-2 with imperfect serological tests: Exploiting cutoff-free approaches

Abstract

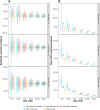
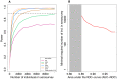
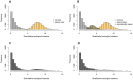
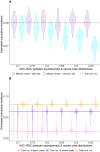
Large-scale serological testing in the population is essential to determine the true extent of the current SARS-CoV-2 pandemic. Serological tests measure antibody responses against pathogens and use predefined cutoff levels that dichotomize the quantitative test measures into sero-positives and negatives and use this as a proxy for past infection. With the imperfect assays that are currently available to test for past SARS-CoV-2 infection, the fraction of seropositive individuals in serosurveys is a biased estimator of the cumulative incidence and is usually corrected to account for the sensitivity and specificity. Here we use an inference method-referred to as mixture-model approach-for the estimation of the cumulative incidence that does not require to define cutoffs by integrating the quantitative test measures directly into the statistical inference procedure. We confirm that the mixture model outperforms the methods based on cutoffs, leading to less bias and error in estimates of the cumulative incidence. We illustrate how the mixture model can be used to optimize the design of serosurveys with imperfect serological tests. We also provide guidance on the number of control and case sera that are required to quantify the test's ambiguity sufficiently to enable the reliable estimation of the cumulative incidence. Lastly, we show how this approach can be used to estimate the cumulative incidence of classes of infections with an unknown distribution of quantitative test measures. This is a very promising application of the mixture-model approach that could identify the elusive fraction of asymptomatic SARS-CoV-2 infections. An R-package implementing the inference methods used in this paper is provided. Our study advocates using serological tests without cutoffs, especially if they are used to determine parameters characterizing populations rather than individuals. This approach circumvents some of the shortcomings of cutoff-based methods at exactly the low cumulative incidence levels and test accuracies that we are currently facing in SARS-CoV-2 serosurveys.

Fig 1. Point-estimates of cumulative incidence using the cutoff-based methods and the mixture model.

Each violin represents 50 in silico serosurveys conducted with cohorts of 10, 000 virtual individuals and the points represent the median values. (A) Point-estimates of the cumulative incidence. The dashed line indicates the true cumulative incidence we assumed in the simulations. Please note that the scale of the y-axis differs between the sub-figures. (B) Size of the 95% uncertainty intervals. For the Rogan-Gladen and mixture-model estimates, the uncertainty intervals are the 95% confidence intervals, which we calculated with the bootstrap method (see Methods). For the Bayesian estimators, the uncertainty interval are the 95% credible intervals.

Fig 2. Estimated fold increases in cumulative incidence for the cutoff-based methods and the mixture model.

In the simulated serosurveys, we assumed the cumulative incidence to increase from 1.5% to 15%, resulting in a true fold increase of 10 (dashed line). The violins show the distribution of 50 in silico serosurveys for both cumulative incidence levels conducted with cohorts of 10, 000 individuals and a test with an AUC-ROC value of 0.975. The dots indicate the median value.

Fig 3. Statistical power of the mixture model.

In all simulations, the number of control and case data is fixed to 5, 000 each and the true cumulative incidence level is 8%. (A) Statistical power versus the number of individuals in the serosurvey for varying levels of test accuracy (AUC-ROC). The power is calculated as the fraction of simulated serosurveys that resulted in a cumulative incidence estimate that is within 25% of the true cumulative incidence and for which the true cumulative incidence level lies within 2 standard deviations of the estimated value. Each point in the graph represents the result of 3, 000 in silico serosurveys. (B) The minimal number of virtual individuals necessary to obtain a statistical power of 0.9 over a range of AUC-ROC values.

Fig 4. Effect of varying the number of control and case sera used to calibrate the serological test.

(A) An example of the true distribution (solid lines) of the control (grey) and case (orange) sera, the data simulated from those distributions (histograms) and the inferred densities (dashed lines) used in the inference of the cumulative incidence. Here, 150 control and case sera have been simulated and the AUC-ROC value of the test is equal to 0.975. (B) Point estimates of cumulative incidence for various numbers of control and case sera used to calibrate the serological test and three AUC-ROC values. Each violin shows the distribution of the estimated cumulative incidence of 50 in silico serosurveys conducted with cohorts of 10, 000 virtual individuals. The red line shows the true cumulative incidence we assumed in the simulated serosurveys (8%). (C) Size of the 95% confidence intervals of the estimated cumulative incidences. (D) Statistical power versus the number of control and case sera used in the validation data for varying levels of test accuracy (AUC-ROC). Each point in the graph represents the result of 3, 000 in silico serosurveys. (E) The minimal number of virtual individuals necessary to obtain a statistical power of 0.9 over a range of number of control and case sera in the validation data.

Fig 5. Conceptual figure on how a discrepancy between the test validation and serosurvey data can be detected.

(A) Histograms of simulated validation data from controls and severe cases. (B) Histograms of simulated validation data from controls and severe and asymptomatic cases. (C) Histogram of simulated serosurvey data when all infections in a population are severe. (D) Histogram of simulated serosurvey data when one third of all cases is asymptomatic and two thirds severe.

Fig 6. Estimates of the cumulative incidence in a population where individuals have been uninfected, as well as symptomatically and severely infected.

The x-axes represent the AUC-ROC value between the asymptomatic and severe case distribution. The AUC-ROC value between the control and the severe case distributions is 1. Each violin represents the result of 50 simulated serosurveys with 10, 000 individuals per serosurvey. The true total cumulative incidence of severe and asymptomatic infections is 10%, of which 20% are asymptomatic. (A) Cyan violins show estimates of the total cumulative incidence based on an inferred case distribution containing only severe case sera, whereas purple violins show estimates where the case distribution is containing both asymptomatic and severe case sera. (B) The estimated cumulative incidence of the mild (light purple) and the severe (dark purple) cases, where the case sera distribution is only based on severe cases, but the likelihood equation also estimates the shape of the asympotomatic cases and their relative prevalence.

Fig 7. Conceptual diagram of the distribution of the quantitative test measures for control and case sera.

(A) Hypothetical probability density of quantitative test measures of control sera and three possible case sera distributions. (B) ROC-curves corresponding to the distribution of quantitative test measures of the control sera and each of the possible distributions for the case sera. (C) Visualization of the ‘maximal Youden’ and ‘high specificity’ cutoffs. (D) Visualization of the ‘maximal Youden’ and ‘high specificity’ cutoffs in the ROC curves.