Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nano-cavities: Application to study of biological systems
- PMID: 33636633
- PMCID: PMC8889562
- DOI: 10.1016/j.jmr.2021.106933
Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nano-cavities: Application to study of biological systems
Abstract
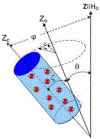
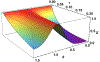
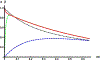
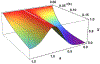
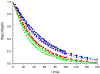
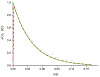
We analyze the application of the spin locking method to study the spin dynamics and spin-lattice relaxation of nuclear spins-1/2 in liquids or gases enclosed in a nano-cavity. Two cases are considered: when the amplitude of the radio-frequency field is much greater than the local field acting the nucleus and when the amplitude of the radio-frequency field is comparable or even less than the local field. In these cases, temperatures of two spin reservoirs, the Zeeman and dipole ones, change in different ways: in the first case, temperatures of the Zeeman and dipolar reservoirs reach the common value relatively quickly, and then turn to the lattice temperature; in the second case, at the beginning of the process, these temperatures are equal, and then turn to the lattice temperature with different relaxation times. Good agreement between the obtained theoretical results and the experimental data is achieved by fitting the parameters of the distribution of the orientation of nanocavities. The parameters of this distribution can be used to characterize the fine structure of biological samples, potentially enabling the detection of degradative changes in connective tissues.
Keywords: Nano-cavity; Spin locking; Spin-lattice relaxation; Zeeman and dipolar reservoirs.
Copyright © 2021 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures


Similar articles
-
Spin locking in liquid entrapped in nanocavities: Application to study connective tissues.J Magn Reson. 2019 Feb;299:66-73. doi: 10.1016/j.jmr.2018.12.012. Epub 2018 Dec 15. J Magn Reson. 2019. PMID: 30580046 Free PMC article.
-
Spin-lattice relaxation in liquid entrapped in a nanocavity.J Magn Reson. 2020 Feb;311:106669. doi: 10.1016/j.jmr.2019.106669. Epub 2019 Dec 16. J Magn Reson. 2020. PMID: 31881481 Free PMC article.
-
Anisotropy of spin-spin and spin-lattice relaxation times in liquids entrapped in nanocavities: Application to MRI study of biological systems.J Magn Reson. 2016 Feb;263:71-78. doi: 10.1016/j.jmr.2015.12.015. Epub 2016 Jan 4. J Magn Reson. 2016. PMID: 26773529
-
Self-diffusion studies by intra- and inter-molecular spin-lattice relaxometry using field-cycling: Liquids, plastic crystals, porous media, and polymer segments.Prog Nucl Magn Reson Spectrosc. 2017 Aug;101:18-50. doi: 10.1016/j.pnmrs.2017.04.001. Epub 2017 Apr 9. Prog Nucl Magn Reson Spectrosc. 2017. PMID: 28844220 Review.
-
High-field EPR on membrane proteins - crossing the gap to NMR.Prog Nucl Magn Reson Spectrosc. 2013 Nov;75:1-49. doi: 10.1016/j.pnmrs.2013.07.002. Epub 2013 Jul 29. Prog Nucl Magn Reson Spectrosc. 2013. PMID: 24160760 Review.
Cited by
-
Anisotropy of transverse and longitudinal relaxations in liquids entrapped in nano- and micro-cavities of a plant stem.J Magn Reson. 2021 Oct;331:107051. doi: 10.1016/j.jmr.2021.107051. Epub 2021 Aug 18. J Magn Reson. 2021. PMID: 34455368 Free PMC article.
-
Determining the internal orientation, degree of ordering, and volume of elongated nanocavities by NMR: Application to studies of plant stem.J Magn Reson. 2022 Aug;341:107258. doi: 10.1016/j.jmr.2022.107258. Epub 2022 Jun 17. J Magn Reson. 2022. PMID: 35753185 Free PMC article.
-
Anisotropy of Transverse Spin Relaxation in H2O-D2O Liquid Entrapped in Nanocavities: Application to Studies of Connective Tissues.Hyperfine Interact. 2021 Dec;242(1):19. doi: 10.1007/s10751-021-01731-9. Epub 2021 Oct 30. Hyperfine Interact. 2021. PMID: 35990926 Free PMC article.
References
-
- Abragam A, The Principles of Nuclear Magnetism, Oxford Clarendon Press, 1961.
-
- de Gennes PG and Prost J, The Physics of Liquid Crystals, Oxford Clarendon Press, 1995.
-
- Callaghan PT, Principles of Nuclear Magnetic Resonance Microscopy, Oxford Clarendon Press, 1991.
-
- Breitmaier E, Structure Elucidation by NMR in Organic Chemistry: A Practical Guide, John Wiley&Sons Ltd., 2002
-
- Alba-Simionesco C, Coasne B, Dosseh G, Dudziak G, Gubbins KE, Radhakrishnan R. and Sliwinska-Bartkowiak M, Effects of confinement on freezing and melting, J. Phys.: Condens. Matter 18 R15 (2006). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

