A stable, unified model for resonant Faraday cages

Abstract

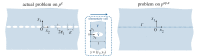
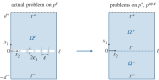
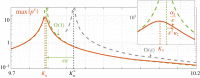
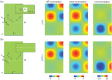
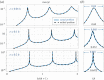
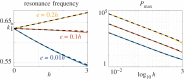
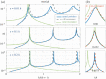
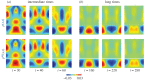
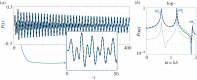
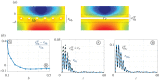
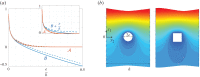
We study some effective transmission conditions able to reproduce the effect of a periodic array of Dirichlet wires on wave propagation, in particular when the array delimits an acoustic Faraday cage able to resonate. In the study of Hewett & Hewitt (2016 Proc. R. Soc. A 472, 20160062 (doi:10.1098/rspa.2016.0062)) different transmission conditions emerge from the asymptotic analysis whose validity depends on the frequency, specifically the distance to a resonance frequency of the cage. In practice, dealing with such conditions is difficult, especially if the problem is set in the time domain. In the present study, we demonstrate the validity of a simpler unified model derived in Marigo & Maurel (2016 Proc. R. Soc. A 472, 20160068 (doi:10.1098/rspa.2016.0068)), where unified means valid whatever the distance to the resonance frequencies. The effectiveness of the model is discussed in the harmonic regime owing to explicit solutions. It is also exemplified in the time domain, where a formulation guaranteeing the stability of the numerical scheme has been implemented.

Keywords: asymptotic analysis; high-order homogenization; homogenized boundary conditions; thin periodic interface.

Figure 1.

A linear array in free space (not a cage). Left, the actual problem on p^ε in rescaled coordinate x = x/L. Right, the resulting effective problem on p^ap. The asymptotic homogenization, symbolized by the arrow, involves elementary problems on (Q⁻, Q⁺) set in an elementary cell $\mathsf{Y}$ containing a single wire. (Online version in colour.)

Figure 2.

A linear array on top of a Dirichlet wall Γ⁻. The actual problem (3.1) on p^ε and, as a result of asymptotic analysis, the limit problem (3.2) on p* and of the unified problem (3.3) on p^ap,ε. (Online version in colour.)

Figure 3.

Resonance curve by means of max| p^ε| in the cavity Ω⁻ close to the resonance K_n (solid red line). The dashed grey line shows the off-resonance solution blowing up at resonance K_n* of the close cavity (its validity is limited to p^ε = O(ε)). The dashed green line shows the near-resonance solution blowing up at (K_n* + εκ) close to the actual resonance K_n (its validity is limited to p^ε = O(1)). The inset show the parametrization of the resonance curve in the on-resonance regime whose validity is limited to p^ε = O(1/ε). (Online version in colour.)

Figure 4.

Wavefields in a one-dimensional cage—p(x) computed numerically (a) and p^ap(x) from (4.1) and (4.2) (b). The source is a plane wave of amplitude unity at an oblique incidence of 45^° on a periodic array of square wires with spacing h = 1 and with e = e₁ = e₂ = 0.1 ( x₂ ∈ (0, 10)); the Dirichlet wall Γ is at x₂ = −7. The amplitude within the cavity is O(ε) off-resonance (k = 0.700), O(1) near-resonance (k = 0.640) and O(1/ε) on-resonance (k = 0.633). (Online version in colour.)

Figure 5.

Maximum pressure in the cavity against the dimensionless frequency kh, max|p| from direct numerics (solid blue lines), max| p^ap,ε| from (4.1) and (4.2) (dashed black lines). The panels in (b) show a zoom of the panels in (a). (Online version in colour.)

Figure 6.

Variations of the resonance frequency k₁ and maximum amplitude ${\mathcal{P}}_{\text{max}}$ at the resonance against h. Solid lines, computed from direct numerics; dashed black lines, from (4.1). (Online version in colour.)

Figure 7.

Same representation as in figure 5. Direct numerics for the actual problem and from the iterative model: off-resonance curve from (4.4), near-resonance curve from (4.5) and on-resonance curve from (4.6). (Online version in colour.)

Figure 8.

Snapshots at short times—the p(x, t) solution of the actual problem (a) and of the p^ap(x, t) solution to the effective problem ruled by (5.1) with a = e (b); both p and p^ap are computed numerically. (Online version in colour.)

Figure 9.

The source s(t) (a) and its Fourier transform $\hat{s}(\omega )$ (b); the red arrows show the resonance frequencies of the cage. (Online version in colour.)

Figure 10.

Same representation as in figure 8 at intermediate times (a) and at long times (b). (Online version in colour.)

Figure 11.

(a) Time variation of P(t) (solid blue line) and of P^ap(t) (dashed black line) for t ∈ (0, 400). (b) Corresponding spectra $\hat{P}(\omega )$ and $\widehat{P^{\text{ap}}}(\omega )$; the dotted grey line shows the spectrum of the error | p^ap − p|. (Online version in colour.)

Figure 12.

Numerical instability in the effective problem ruled by unstable conditions (5.1) when a < a_c. (a) Stability diagram for discs and squares. Blue lines show a_c(e) from (5.6) for wires of extent e. The red symbols show an estimate of a_c determined numerically as the lowest value of a producing a stable solution. (b) Exponential growth in the time of |P^ap(t)|, (5.5), for an unstable formulation (a = 0.015 < a_c, solid blue lines) and for a stable formulation (a = 0.033 > a_c, dashed black lines). The inset shows ${\mathcal{E}}^{\text{ap}}(t;a)$ diverging to +∞ and ${\mathcal{E}}_{\mathrm{\Gamma }}(t;a)$ diverging to −∞ for a = 0.015. (Online version in colour.)

Figure 13.

Energies in the actual and effective problems. (a) A zoom of p(x, t₀) and p^ap(x, t₀) in {(x₁, x₂) ∈ ( − 1.5, 1.5) × ( − 3, 3)} (t₀ = 19). (b) The difference between the time-averaged energies ${{\mathcal{E}}^{\text{ap}}}_{{\mathrm{\Omega }}_b}$ and ${\mathcal{E}}_{{\mathrm{\Omega }}_b}$ against b and time variations of the energies for ***** b = e = 0.1 and **** b = 5e = 0.5. (Online version in colour.)

Figure 14.

Relative difference between the time-averaged interface effective energy ${\mathcal{E}}_{\mathrm{\Gamma }}(a)$ and the time-averaged actual energy ${\mathcal{E}}_{{\mathrm{\Omega }}_a}$ against a; time variations of ${\mathcal{E}}_{\mathrm{\Gamma }}(t;a)$ (dashed black lines) and $\mathcal{E}(t;a)$ (solid blue lines) for ***** a = 0.1, **** a = 0.15 and *** a = 0.25. (Online version in colour.)

Figure 15.

Effective fields p^ap(x, t₀) (t₀ = 19) in the vicinity of Γ for a = 0.1, a = 0.16 and a = 0.25 (a) and corresponding profiles of p (solid blue lines) and p^ap (dashed black lines) at x₁ = a (b). (Online version in colour.)

Figure 16.

(a) Effective parameters $(\mathcal{A},\mathcal{B})$ against e/h for squares (solid lines) and for discs (dashed lines); the dotted grey line shows ${\mathcal{A}}_0=-(1/2\pi )\log \mathrm{sin\hspace{0.17em}}(2\pi e/h)$. (b) Examples of solution Q⁺ to the elementary problem (2.3). (Online version in colour.)

Figure 17.

Validity of the thin wire approximation; same representation as in figure 5. Solid blue lines, direct numerics; dashed black lines; unified model with (4.1) and (4.2); and dotted green lines, thin wire model with (4.1); see (C 2). The panels in (b) show a zoom of the panels in (a). (Online version in colour.)