Adaptive mesh refinement and coarsening for diffusion-reaction epidemiological models

Abstract

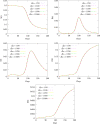
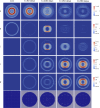
The outbreak of COVID-19 in 2020 has led to a surge in the interest in the mathematical modeling of infectious diseases. Disease transmission may be modeled as compartmental models, in which the population under study is divided into compartments and has assumptions about the nature and time rate of transfer from one compartment to another. Usually, they are composed of a system of ordinary differential equations in time. A class of such models considers the Susceptible, Exposed, Infected, Recovered, and Deceased populations, the SEIRD model. However, these models do not always account for the movement of individuals from one region to another. In this work, we extend the formulation of SEIRD compartmental models to diffusion-reaction systems of partial differential equations to capture the continuous spatio-temporal dynamics of COVID-19. Since the virus spread is not only through diffusion, we introduce a source term to the equation system, representing exposed people who return from travel. We also add the possibility of anisotropic non-homogeneous diffusion. We implement the whole model in libMesh, an open finite element library that provides a framework for multiphysics, considering adaptive mesh refinement and coarsening. Therefore, the model can represent several spatial scales, adapting the resolution to the disease dynamics. We verify our model with standard SEIRD models and show several examples highlighting the present model's new capabilities.

Keywords: Adaptive mesh refinement and coarsening; COVID-19; Compartmental models; Diffusion–reaction; Partial differential equations.

Fig. 1

Statistical refinement strategy: elements in hatched areas are flagged to AMR/C process

Fig. 2

Adaptive mesh refinement: hierarchy of refined meshes with hanging nodes, where the solution is constrained to enforce continuity

Fig. 3

Test 1: Reproducing a compartmental model

Fig. 4

Test 1: Values over a centralized horizontal line at t = 365 days

Fig. 5

Test 2: Infected initial condition

Fig. 6

Test 2: Values over a centralized horizontal line at t = 365 days

Fig. 7

Test 2: Infected people at different time-steps (top) and adapted meshes (bottom)

Fig. 8

Test 3: Susceptible initial condition

Fig. 9

Test 3: Infected people at different time-steps (top) and adapted meshes (bottom)

Fig. 10

Test 3: Total deaths at t = 365 days

Fig. 11

COVID19 Test 1: Compartmental model

Fig. 12

COVID19 Test 2: Initial conditions

Fig. 13

COVID19 Test 2: Reproducing a 1D model

Fig. 14

COVID Test 2: Populations at t = 200 days

Fig. 15

COVID19 Test 2: Mesh convergence study (total population by time)

Fig. 16

COVID19 Test 2: Mesh convergence study (individuals at t = 90 days)

Fig. 17

COVID19 Test 2: Time convergence study (total population by time)

Fig. 18

COVID19 Test 2: Time convergence study (individuals at t = 90 days)

Fig. 19

COVID Test 3: Populations at different times (top rows) and adapted meshes (bottom)

Fig. 20

COVID Test 3: Populations over a horizontal/vertical line crossing the middle of the domain

Fig. 21

COVID Test 3: Time history of the total number of individuals

Fig. 22

COVID Test 4: Populations at different times (top rows) and adapted meshes (bottom)

Fig. 23

COVID Test 4: Populations over a horizontal line crossing the middle of the domain

Fig. 24

COVID Test 4: Populations over a vertical line crossing the middle of the domain

Fig. 25

COVID Test 4: Time history of the total number of individuals

Fig. 26

COVID Test 5: Initial susceptible population

Fig. 27

COVID Test 5: Example of the random source of exposed people

Fig. 28

COVID Test 5: Populations at different times (top rows) and adapted meshes (bottom)

Fig. 29

COVID Test 5: Populations over a horizontal line crossing the middle of the domain

Fig. 30

COVID Test 5: Populations over a vertical line crossing the middle of the domain

Fig. 31

COVID Test 5: Time history of the total number of individuals