Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Apr;26(4):1441-1452.
doi: 10.1109/JBHI.2021.3063106. Epub 2022 Apr 14.

Monitoring and Tracking the Evolution of a Viral Epidemic Through Nonlinear Kalman Filtering: Application to the COVID-19 Case

Antonio Gomez-Exposito, Jose A Rosendo-Macias, Miguel A Gonzalez-Cagigal

Monitoring and Tracking the Evolution of a Viral Epidemic Through Nonlinear Kalman Filtering: Application to the COVID-19 Case

Antonio Gomez-Exposito et al. IEEE J Biomed Health Inform. 2022 Apr.

Abstract

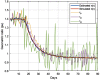
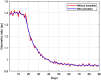
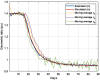
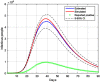
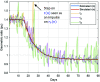
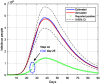
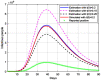
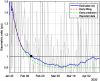
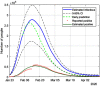
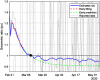
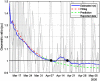
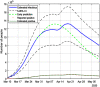
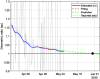
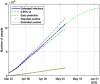
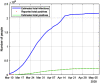
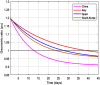
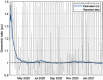
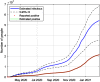
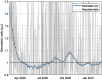
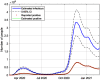
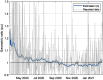
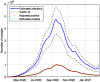
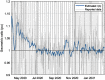
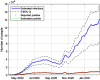
This work presents a novel methodology for systematically processing the time series that report the number of positive, recovered and deceased cases from a viral epidemic, such as Covid-19. The main objective is to unveil the evolution of the number of real infected people, and consequently to predict the peak of the epidemic and subsequent evolution. For this purpose, an original nonlinear model relating the raw data with the time-varying geometric ratio of infected people is elaborated, and a Kalman Filter is used to estimate the involved state variables. A hypothetical simulated case is used to show the adequacy and limitations of the proposed method. Then, several countries, including China, South Korea, Italy, Spain, U.K. and the USA, are tested to illustrate its behavior when real-life data are processed. The results obtained clearly show the beneficial effect of the severe lockdowns imposed by many countries worldwide, but also that the softer social distancing measures adopted afterwards have been almost always insufficient to prevent the subsequent virus waves.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Estimation of r(n) in the base case.
Fig. 2.
Fig. 2.
Estimation of r(n) with and without the smoother.
Fig. 3.
Fig. 3.
Comparison of the proposed method with moving average filters.
Fig. 4.
Fig. 4.
Estimation of the infectious people in the base case.
Fig. 5.
Fig. 5.
Estimation of r(n) with a step on the testing ratio.
Fig. 6.
Fig. 6.
Estimation of the infectious people with a step on the testing ratio.
Fig. 7.
Fig. 7.
Estimation of the infectious people for a range of t(0) values.
Fig. 8.
Fig. 8.
Estimation of r(n) in China in the first period considered.
Fig. 9.
Fig. 9.
Estimation of infectious people in China in the first period considered.
Fig. 10.
Fig. 10.
Estimation of r(n) in South-Korea in the first period considered.
Fig. 11.
Fig. 11.
Estimation of infectious people in South-Korea in the first period.
Fig. 12.
Fig. 12.
Estimation of r(n) in Spain in the first period considered.
Fig. 13.
Fig. 13.
Estimation of infectious people in Spain in the first period considered.
Fig. 14.
Fig. 14.
Estimation of r(n) in U.K. in the first period considered.
Fig. 15.
Fig. 15.
Estimation of infectious people in U.K. in the first period considered.
Fig. 16.
Fig. 16.
Estimation of cumulative infectious people in Spain.
Fig. 17.
Fig. 17.
Fitted geometric ratios from common threshold.
Fig. 18.
Fig. 18.
Estimation of r(n) in USA in the second period considered.
Fig. 19.
Fig. 19.
Estimation of infectious people in USA in the second period considered.
Fig. 20.
Fig. 20.
Estimation of r(n) in Italy in the second period considered.
Fig. 21.
Fig. 21.
Estimation of infectious people in Italy in the second period considered.
Fig. 22.
Fig. 22.
Estimation of r(n) in India in the second period considered.
Fig. 23.
Fig. 23.
Estimation of infectious people in India in the second period considered.
Fig. 24.
Fig. 24.
Estimation of r(n) in Brazil in the second period considered.
Fig. 25.
Fig. 25.
Estimation of infectious people in Brazil in the second period considered.
See this image and copyright information in PMC

References

    1. Rohman A. and Zaber M., “Lockdown vs. Social distancing: Need for effective communication,” Jakarta Post, 2020. [Online]. Available: https://www.thejakartapost.com/academia/2020/05/19/lockdown-vs-social-di...
    1. Pueyo T., “Coronavirus: Why you must act now,” 2020. [Online]. Available: https://medium.com/@tomaspueyo/coronavirus-act-today-or-people-will-die-...
    1. Imperial College COVID-19 response team. “Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand,” 2020. [Online]. Available: https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-... - PMC - PubMed
    1. Kermack W. O. and McKendrick A. G., “A contribution to the mathematical theory of epidemics,” Proc Roy. Soc Math Phys Eng Sci., vol. 115, no. 772, pp. 700–721, 1927.
    1. Giordano G. et al., “Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy,” Nat Med., vol. 26, pp. 855–860, 2020. doi: 10.1038/s41591-020-0883-7. - DOI - PMC - PubMed

Publication types