Suppressing evolution in genetically engineered systems through repeated supplementation

Abstract

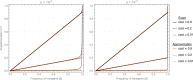
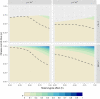
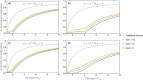
Genetically engineered organisms are prone to evolve in response to the engineering. This evolution is often undesirable and can negatively affect the purpose of the engineering. Methods that maintain the stability of engineered genomes are therefore critical to the successful design and use of genetically engineered organisms. One potential method to limit unwanted evolution is by taking advantage of the ability of gene flow to counter local adaption, a process of supplementation. Here, we investigate the feasibility of supplementation as a mechanism to offset the evolutionary degradation of a transgene in three model systems: a bioreactor, a gene drive, and a transmissible vaccine. In each model, continual introduction from a stock is used to balance mutation and selection against the transgene. Each system has its unique features. The bioreactor system is especially tractable and has a simple answer: The level of supplementation required to maintain the transgene at a frequency $\hat{p}$ is approximately $\hat{p}s$ , where s is the selective disadvantage of the transgene. Supplementation is also feasible in the transmissible vaccine case but is probably not practical to prevent the evolution of resistance against a gene drive. We note, however, that the continual replacement of even a small fraction of a large population can be challenging, limiting the usefulness of supplementation as a means of controlling unwanted evolution.

Keywords: bioreactor; gene drive; gene flow; genetic engineering; swamping; transmissible vaccine.

FIGURE 1

The level of per‐generation supplementation (σ) required to maintain an equilibrium frequency (p*) of a transgene with a selective cost of s in a chemostat bioreactor. The orange curves represent the approximation σ ≈ p s. Mutation rates (μ) are per generation and were chosen to highlight the differences between the exact and approximate solutions at extremes, but the rates also span potentially reasonable values under different engineering designs (Sleight et al., 2010; Williams, 2014)

FIGURE 2

The strategy of bioreactor supplementation by replacement of the entire culture when transgene frequency (p) drops below a threshold. In each of the four panels, Equation 3 was initialized with a starting frequency (p ₀) of 1 − μ and time advanced until p fell below 0.8 In the following generation, the culture was discarded and replaced with a new population at the same starting frequency as the first trial. Panels within a row vary mutation rate; panels within a column vary selection (disadvantage of transgene carriage)

FIGURE 3

Supplementation necessary to achieve a peak gene drive allele frequency of ≥95% for differing mutation and drive conversion efficiencies (c). Text Equations (4) and (5) were iterated across 100 generations assuming a starting frequency of 1 × 10⁻⁶ for both the gene drive and resistance mutations. The hashed area delineates parameter combinations where the drive fails to reach the target frequency regardless of supplementation effort. The dashed lines show the boundary region above which nonzero supplementation was required for the drive to reach the target threshold

FIGURE 4

Supplementation to avert evolution of resistance to a gene drive has little effect on the maximum frequency attained by a gene drive, but it hastens gene drive evolution and suppresses final resistance allele frequency. The frequency of both drive and drive‐resistant alleles over time is shown, obtained by iterating Equations (4) and (5) for 100 generations. In the top row (panels a and b), the gene drive efficiency was set to 0.95; in the lower row (panels c and d), it was set to 0.7. The mutation rates from wild‐type to resistant alleles were 1 × 10⁻⁷ in the first column (a,c) and 1 × 10⁻⁴ in the second column (b, d). These numbers were chosen from previously estimated mutation rates for a gene drive in Drosophila melanogaster (10^–4 to 10^–8) and span decay rates (0.6 * 10^–6 to 1.7 * 10^–6) of inserted lacI in transgenic mice (Edgington & Alphey, 2019; Kohler et al., 1991). In all cases, the selection acting against drive homozygotes was s = 0.7. Simulations were started with the resistant allele already present in the population at a frequency of 10^–7

FIGURE 5

Susceptible–infectious–recovered (SIR) model flow chart for a transgenic transmissible vaccine with antigenic decay. This figure accompanies text Equations (6)–(10)

FIGURE 6

The amount of direct vaccination necessary to protect a population from invasion by a pathogen of different R ₀’s (the text indicates how R ₀ is calculated from parameters). A mutation‐free vaccine would outgrow the pathogen (and needs no supplementation) up to the point that the pathogen R ₀ exceeds the vaccine R ₀. Beyond that, increasing levels of supplementation are required to offset higher levels of pathogen R ₀. Those effects are purely demographic. The magnitude and effect of vaccine evolution in this system is determined by the mutation rate and selective cost of carrying the transgene. It is seen that vaccine evolution invariably increases the required supplementation, from the effects of both mutation and selection, but the effects can be relatively modest against the background of supplementation required in the absence of evolution. Figure results universally use a birth rate of b = 10, a death rate of d = 0.01, and a recovery rate of γ_v = 0.1. The cost of carrying the antigen was calculated as 1 − R _{0 ,v}/R _{0 ,w} which describes the relative decrease in reproductive number resulting from carrying an antigen. The method of calculating the level of direct vaccination to protect a population against invasion is given in the Appendix 1