A Dynamic Motion Analysis of a Six-Wheel Ground Vehicle for Emergency Intervention Actions

Abstract

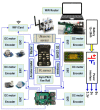
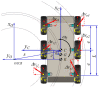
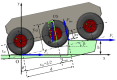
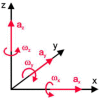
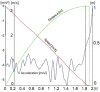
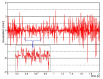
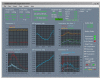
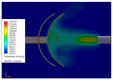
To protect the personnel of the intervention units operating in high-risk areas, it is necessary to introduce (autonomous/semi-autonomous) robotic intervention systems. Previous studies have shown that robotic intervention systems should be as versatile as possible. Here, we focused on the idea of a robotic system composed of two vectors: a carrier vector and an operational vector. The proposed system particularly relates to the carrier vector. A simple analytical model was developed to enable the entire robotic assembly to be autonomous. To validate the analytical-numerical model regarding the kinematics and dynamics of the carrier vector, two of the following applications are presented: intervention for extinguishing a fire and performing measurements for monitoring gamma radiation in a public enclosure. The results show that the chosen carrier vector solution, i.e., the ground vehicle with six-wheel drive, satisfies the requirements related to the mobility of the robotic intervention system. In addition, the conclusions present the elements of the kinematics and dynamics of the robot.

Keywords: dynamic; kinematic; mobile robotics; mobility; rescue; sensors; wheel.

Figure 1

The terrestrial 6 × 6 robot developed for identifying, monitoring, and intervening in risky areas. The structural elements of the robot include the command-and-control system, the battery system, and the weather station.

Figure 2

Schematic representation of the three major classes of command-and-control systems of terrestrial robots. For ongoing research, on the use of 6 × 6 terrestrial robots for the purpose of identification, monitoring and intervention in risk areas, we proposed that of the three versions: (a) direct or manual control; (b) mixed control; (c) supervised control, to use version (b).

Figure 3

The control and command architecture of the studied robot including obstacle detection (ultrasonic and infrared (IR) sensors); orientation (tri-axial accelerometer and global positioning system (GPS)), gyroscope (pitch, yaw, and roll), compass; DC motor encoder, Electronic Speed Controller (ESC); Pixhawk controller, Raspberry Pi 4 controller and NVIDIA Jetson Nano; power system, and Wi-Fi communication system.

Figure 4

Schematic representation of the propulsion system of the 6 × 6 robot for emergency situations consists of six motors with a gearbox, six wheels with rubber tires, and a nodular balloon inflated with air for more efficient damping of the unevenness of the route during movement of the robot.

Figure 5

The 6 × 6 kinematic diagrams of the robot showing the following essential characteristics for a simple and fast analysis of the robot kinematics: the six driving wheels are not steering wheels; turns are made by changing the rotational speeds of the six wheels; cornering radii varied depending on the rotational speed of the drive wheels and the indices of adhesion to the ground, the slip indices. If the movement was rectilinear, the decomposition of the speed was uniform only for the ideal conditions of movement; the ground contact of the balloon of the wheels was related to the pressure in the balloon. The weight of the robot and the position of the center of gravity may be altered, in particular, by the operating platforms.

Figure 6

Schematic of the 2D dynamics of the 6 × 6 robot, which had some specificities related to the choice of travel mode. The ground contact spots of the six wheels were identical. Working conditions are ideal when Md = Mr (Md—motor torque; Mr—resistant moment). The geometric center of the contact spots (yellow dots) during the turn is represented outside the geometric center of the contact spots. This representation suggests that progression in the field is influenced by different coefficients and that each operational platform can create an additional balance.

Figure 7

A schematic of the 3D dynamics of the 6 × 6 robot showing the elements that influence the dynamic characteristics of a land vehicle: air resistance, friction force, robot weight, center of gravity position, wheel radius, and slope angle. The following figures will highlight other elements that contribute to influencing the law of motion of the robot.

Figure 8

Schematic of the escalation of a step-type obstacle by the robot. To ensure good ability to climb the step, the front, and middle wheels to be in permanent contact with the step to be climbed. It is not mandatory to have this situation; depending on the geometry of the workspace, energy consumption can increase, which affects the autonomy of movement. The robot was designed to move without being powered by a cable.

Figure 9

The variation in $\mathsf{\beta }\hspace{0.33em}\left[grd\right]$ as a function of the center of mass for h = 0.20 m (where h is the height of the step obstacle); the height of the step is constant. If the step to be scaled has a different height, the values in the graph will change. The pressure value of the wheel tires was not considered in this simulation.

Figure 10

The variation in the $\mathsf{\mu }\hspace{0.33em}\left[-\right]$ necessary for climbing a slope following the simulation using Equations (15)–(19). For the geometric characteristics of the robot and the total minimum adhesion coefficient, the robot could climb a step under the conditions of a CG (center of gravity of the robot) with a height = 0.20 m.

Figure 11

The variation in the necessary $M_t\hspace{0.33em}\left[Nm\right]$ as a function of the tilt angle of the slope.

Figure 12

The variation in the $\mathsf{\mu }\hspace{0.33em}\left[-\right]$ necessary to cross an obstacle as a function of its height. The data used for the calculations are found in Appendix A and Table A1. Given the geometric characteristics of the towing robot and the mobile platform, and that changes are possible depending on the dimensions of the operational platforms, the robot can be used for different missions; we consider the data used to be sufficient: (a) crossing with bridge 1; (b) crossing with bridges 1 and 2.

Figure 13

The variation in the $F_t\hspace{0.33em}\left[N\right]$ necessary for crossing an obstacle as a function of its height. The explanations presented in Figure 12 also apply here: (a) crossing with bridge 1; (b) crossing with bridges 1 and 2.

Figure 14

Schematic of braking while descending a longitudinal slope. The dynamics of the robot during braking are much more suggestive when the process is diagrammed during the descent of a slope. In this case, two other notions intervene: a, deceleration when braking; $R_f$, friction force.

Figure 15

The variation in the maximum deceleration at braking on a 30º slope as a function of the center of mass.

Figure 16

Basic reference system for inertial navigation.

Figure 17

The dynamic characteristics of the 6 × 6 robot when braking on the slope, determined with the help of an inertial sensor system.

Figure 18

Representation of the displacement of the coordinate system with the help of Euler’s angles.

Figure 19

The evolution of the longitudinal acceleration while braking on a slope, determined with the help of a GPS sensor system.

Figure 20

Fire extinguishing system with two fire extinguishers and mechanism for maintaining the pressure of the extinguishing-type powder (Florex, E.12, Carbo, based on KHCO₃).

Figure 21

Extinguishing jet performance. The fire was maintained by a pile of cotton cloths soaked in liquid fuel or diesel. When the smoke became sufficient and the wind direction changed toward the robot, the smoke sensors triggered the fire extinguishing system. The system was constructed with the help of two inert gas fire extinguishers.

Figure 22

Environmental samples taken with an Arduino-controlled weather station p/n 80,422. The values recorded by the weather station correspond to a summer period.

Figure 23

Air temperature simulation for an output speed of 10 m/s. The numerical simulation was performed using the finite element simulation application Solid Works.

Figure 24

Thermal study for target C (front view) direct contact with the flame at a temperature above 150 °C. Plate thickness: 4 mm, material: 316 L stainless steel, holding time: 4 min, and a concave shape.

Figure 25

Robotic system with an operational vector used to determine gamma radiation. The experiments were recorded at Titu Maiorescu University in Bucharest.

Figure 26

Gamma radiation measurement with a Canberra dosimeter and spectrometer. The recorded values were part of the background of natural radiation. The values that stood out were specific to potassium. The purpose of data collection was to demonstrate the robot’s ability to perform different missions.