Variance and limiting distribution of coalescence times in a diploid model of a consanguineous population
- PMID: 33675872
- PMCID: PMC8489744
- DOI: 10.1016/j.tpb.2021.02.002
Variance and limiting distribution of coalescence times in a diploid model of a consanguineous population
Abstract
Recent modeling studies interested in runs of homozygosity (ROH) and identity by descent (IBD) have sought to connect these properties of genomic sharing to pairwise coalescence times. Here, we examine a variety of features of pairwise coalescence times in models that consider consanguinity. In particular, we extend a recent diploid analysis of mean coalescence times for lineage pairs within and between individuals in a consanguineous population to derive the variance of coalescence times, studying its dependence on the frequency of consanguinity and the kinship coefficient of consanguineous relationships. We also introduce a separation-of-time-scales approach that treats consanguinity models analogously to mathematically similar phenomena such as partial selfing, using this approach to obtain coalescence-time distributions. This approach shows that the consanguinity model behaves similarly to a standard coalescent, scaling population size by a factor 1-3c, where c represents the kinship coefficient of a randomly chosen mating pair. It provides the explanation for an earlier result describing mean coalescence time in the consanguinity model in terms of c. The results extend the potential to make predictions about ROH and IBD in relation to demographic parameters of diploid populations.
Keywords: Coalescent; Consanguinity; Separation-of-time-scales.
Copyright © 2021 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures

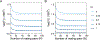
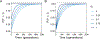

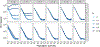
References
-
- CAMPBELL RB, 2015The effect of inbreeding constraints and offspring distribution on time to the most recent common ancestor. Journal of Theoretical Biology 382: 74–80. - PubMed
-
- CHANG JT, 1999Recent common ancestors of all present-day individuals. Advances in Applied Probability 31: 1002–1026.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

