Rethinking delusions: A selective review of delusion research through a computational lens

Abstract

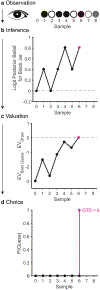
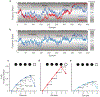
Delusions are rigid beliefs held with high certainty despite contradictory evidence. Notwithstanding decades of research, we still have a limited understanding of the computational and neurobiological alterations giving rise to delusions. In this review, we highlight a selection of recent work in computational psychiatry aimed at developing quantitative models of inference and its alterations, with the goal of providing an explanatory account for the form of delusional beliefs in psychosis. First, we assess and evaluate the experimental paradigms most often used to study inferential alterations in delusions. Based on our review of the literature and theoretical considerations, we contend that classic draws-to-decision paradigms are not well-suited to isolate inferential processes, further arguing that the commonly cited 'jumping-to-conclusion' bias may reflect neither delusion-specific nor inferential alterations. Second, we discuss several enhancements to standard paradigms that show promise in more effectively isolating inferential processes and delusion-related alterations therein. We further draw on our recent work to build an argument for a specific failure mode for delusions consisting of prior overweighting in high-level causal inferences about partially observable hidden states. Finally, we assess plausible neurobiological implementations for this candidate failure mode of delusional beliefs and outline promising future directions in this area.

Keywords: Beads task; Computational psychiatry; Delusions; Inference; Psychosis; Schizophrenia.

Fig. 1.

Distinct, nested processes linking inference and sampling decisions in the POMDP framework. For (a) a sequence of observed samples (grayed-out samples reflect future samples that the agent never sees), this instantiation of the POMDP model shows (b) the logit posterior beliefs of the ideal Bayesian observer (ω₁ = ω₂ = 1) after each sample and (c) the difference in expected value between the best guess (the guess associated with the jar that has highest expected value) and drawing another sample. (d) A stopping decision is made when the expected value of the best guess is higher than the expected value of drawing another sample, i.e., the first point at which the difference in expected values is above 0. This point represents the optimal draws-to-decision (DTD). Note that it takes the optimal agent 6 samples (draws) to reach the stopping point based on valuation, even though the exact same level of belief certainty was achieved after only 4 samples (draws). This illustrates that DTD depends on value-related factors beyond inference. The simulation uses cost parameters (starting endowment of $30; $0 for a correct response; −$15 for an incorrect response; −$0.30 for a draw) consistent with the experimental parameters from Baker et al. (2019).

Fig. 2.

Dynamic effects of prior weighting on inference and relevance to the form of delusions. (a) Long-term trajectory of beliefs with respect to a black jar (in probability space) for two agents (higher ω₁ = 0.995; lower ω₁ = 0.950; ω₂ = 1 for both agents) over 450 randomly selected samples (with replacement) in the beads task. Here, and in general, please note that parameter values were selected to illustrate the belief-updating effects highlighted in the main text. The correct (black) jar has a ratio of 55 black beads to 45 white beads, reflecting an ambiguous situation of weak sensory evidence (likelihood of 0.55). This simulation illustrates an ω₁-driven rigidity effect, whereby the beliefs of the higher-ω₁ agent take more disconfirmatory samples to return to an uncertain level, and a concomitant certainty effect, whereby its beliefs tend to be more certain, relative to the lower-ω₁ agent. (b) Long-term trajectory of beliefs with respect to a black jar (in probability space) for two agents (higher-ω₂ = 1; lower-ω₂ = 0.40; ω₁ = 0.95 for both agents) over the same 450 randomly selected samples in (a) in the beads task. For reference, the higher-ω₂ agent in (b) is identical to the lower-ω₁ agent in (a). Changes in ω₂ induce a certainty effect, i.e., the higher-ω₂ agent tends to reach more certain beliefs than the lower-ω₂ agent, but has no effect on belief rigidity. (c, d, e) Simulations illustrating local belief-updating dynamics over 5 samples for a (c) lower-ω₁ agent (ω₁= 0.70; ω₂ = 1; similar to healthy individuals in Baker et al.), a (d) higher-ω₁ agent (ω₁ = 0.98; ω₂ = 1; consistent with delusional patients in Baker et al.), and a (e) lower-ω₂ agent (ω₁ = 0.70; ω₂ = 0.40). The dotted diagonal lines depict the “leak” of logit prior beliefs and their endpoints indicate the value of the weighted prior for the next belief update. The solid horizontal line is a reference to indicate the value of the unweighted prior. Thus, the distance between the solid line and the dotted line reflects the magnitude of the prior leak for each update. The dashed vertical lines reflect the contribution of the logit likelihood (LLR) to the belief update. It is apparent in (a) that for lower-ω₁ agents, prior beliefs “leak” more, gradually decreasing the magnitude of belief updates over samples leading to relatively less certain and less rigid beliefs; and (b) shows that these effects are attenuated for higher-ω₁ agents, leading to relatively more certain and more rigid beliefs. Comparing (a) and (c) highlights that differences in ω₂ only scale belief certainty and do not affect belief rigidity.

Fig. 3.

Evidence-order effects on belief updating and draws-to-decision under the weighted Bayesian model. (a, b) Simulation of logit posterior beliefs favoring the black jar for a higher-ω₁ agent (ω₁ = 0.98) and a lower-ω₁ agent (ω₁ = 0.70) in two sequences. In (a) evidence favoring the black jar (the correct jar) occurs earlier in the sequence, and the higher-ω₁ agent generally exhibits more certain beliefs than the lower ω₁ agent that the majority black jar is the correct jar. In (b) evidence favoring the black jar occurs later in the sequence, and the higher-ω₁ agent instead exhibits less certain beliefs than the lower-ω₁ agent. Note that parameters were selected to visually exaggerate the effects of interest, although their generality is addressed in the main text. (c) Simulations for various sequence orders including the same samples of evidence show order-dependent differences in beliefs (in probability space) on a sample-by-sample basis between a higher-ω₁ (ω₁ = 0.98; similar to delusional patients in Baker et al.) and a lower-ω₁ agent (ω₁ = 0.89; ω₂ = 1 for all simulations). Positive values (shades of red) in the heatmap indicate that the higher-ω₁ agent exhibits more certain beliefs than the lower-ω₁ agent that the black jar was the correct jar, and negative values (shades of blue) indicate that the lower-ω₁ agent was more certain. (d, e) Simulations of the POMDP valuation process comparing two agents (the same agents from 3c) across different sequences to illustrate how evidence order affects sampling (draws-to-decision) behavior. The remaining POMPD parameters are equivalent to those in Fig. 1 except for the cost of drawing a bead (here $0.10 instead of $0.30 for illustrative purposes). Note that DTD differences between the two agents are opposite between the two sequences. The asterisk in d indicates the point at which the lower-ω₁ agent is forced to make a guess because the maximum number of samples is 8 (as in the Baker et al. task). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)