Biochemical and phylogenetic networks-II: X-trees and phylogenetic trees
- PMID: 33678934
- PMCID: PMC7914393
- DOI: 10.1007/s10910-020-01195-2
Biochemical and phylogenetic networks-II: X-trees and phylogenetic trees
Abstract
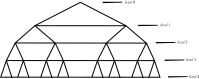
The present study, which is a continuation of the previous paper, augments a recent work on the use of phylogenetic networks. We develop techniques to characterize the topology of various X-trees and binary trees of biological and phylogenetic interests. We have obtained the results for various k-level X-trees and phylogenetic networks with variants of Zagreb, Szeged, Padmakar-Ivan, Schultz and Atom Bond Connectivity topological indices.
Keywords: Biochemical and phylogenetic networks; Eccentricity-based topological indices; Topological indices of X-trees and phylogenetic trees.
© Springer Nature Switzerland AG 2021.
Conflict of interest statement
Conflict of interestThe authors declare that there is no conflict of interests regarding the publication of this paper.
Figures
References
-
- Balasubramanian K. Tree pruning method and lattice statistics on bethe lattices. J. Math. Chem. 1988;2:69–82. doi: 10.1007/BF01166469. - DOI
-
- Balasubramanian K. Nested wreath groups and their applications to phylogeny in biology and Cayley trees in chemistry and physics. J. Math. Chem. 2017;55(1):195–222. doi: 10.1007/s10910-016-0680-1. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources