Trends in Haptic Communication of Human-Human Dyads: Toward Natural Human-Robot Co-manipulation

Abstract

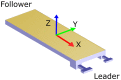
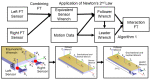
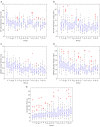
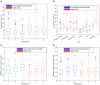
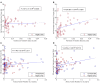
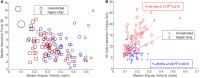
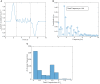
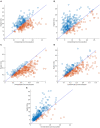
In this paper, we analyze and report on observable trends in human-human dyads performing collaborative manipulation (co-manipulation) tasks with an extended object (object with significant length). We present a detailed analysis relating trends in interaction forces and torques with other metrics and propose that these trends could provide a way of improving communication and efficiency for human-robot dyads. We find that the motion of the co-manipulated object has a measurable oscillatory component. We confirm that haptic feedback alone represents a sufficient communication channel for co-manipulation tasks, however we find that the loss of visual and auditory channels has a significant effect on interaction torque and velocity. The main objective of this paper is to lay the essential groundwork in defining principles of co-manipulation between human dyads. We propose that these principles could enable effective and intuitive human-robot collaborative manipulation in future co-manipulation research.

Keywords: co-manipulation; dyad; haptic communication; human-human interaction (HHI); interaction force/torque; physical human-robot interaction (pHRI); robotics; visual communication.

Figure 1

The orientation of the board with red being the X or anterior direction, green being the Y or lateral direction, and blue representing the Z or superior direction. The leader takes the side with the blue handles and the follower takes the opposite side with no handles. The force/torque sensors are attached between the handles and the table.

Figure 2

A time-lapse of each task in the study. Colored boxes represent the position of the board at each time step with the colors ranging from green for start to red for the finishing position. The dyad at the start and end positions are also shown for clarity. The tasks are referred to as follows: (A) pick and place task, (B) rotation and translation, (C) pure translation, (D) pure rotation, and (E) the 3D complex task. The 3D complex task is split into two panels for clarity. The first half of the 3D Complex task required the dyad to walk across the room. The second part of the task required them to lift the board up and over the first obstacle, lower the board underneath the second obstacle and return to the starting position. The second half of the 3D complex task has the trailing and leading edge labeled and colored black and white for clarity.

Figure 3

The process of transforming the raw force/torque (FT) data from each sensor into the individual leader and follower FT. The top of the figure explains the process of obtaining the data and the bottom row represents a free-body diagram of the board for each set of calculations. The raw FT sensor data was taken from both the FT sensors (the right and left sides of the leader's end of the board) and was represented equivalently as a single equivalent wrench called the equivalent sensor wrench. The equivalent sensor wrench combined with the inertia and known acceleration of the board allowed for the solution of the individual forces and torques of the follower and leader. This calculation was only valid while the board does not experience any external contact forces (i.e., the calculations were invalid when the board was touching the floor, so the data was cropped to only include data where the board was completely lifted off of the floor).

Figure 4

Boxplots showing the distribution of the proposed metrics according to each group. No data exists for groups 1 and 2. (A,B) Depict the 95th percentile interaction force and torque (FT), respectively, between the dyads. (C,D) Show the distribution of median linear and angular velocity for each dyad. (E) Illustrates the difference in completion times for all of the dyads. The groups were sorted by increasing completion times and so it should be noted that the trend for median linear and angular velocity were opposite of the trend for completion time.

Figure 5

A scatter plot of the median linear velocity (A) and median angular velocity (B), as a function of completion time. The tasks are all delineated by different shapes and colors. A strong correlation between linear velocity and completion time should be noted.

Figure 6

Boxplots showing the distribution of completion times divided by repetition (A,B). It should be noted that the haptic-only communication (HC) complex task was significantly longer in completion time than the other tasks. The translation task with unrestricted communication (UC) also was significantly shorter than the other tasks. (C,D) Show boxplots of the distribution of median linear and angular velocity for each repetition. In (A,C,D), a significant amount of learning can be perceived between the dyad in terms of the reduction in completion time and the increase in speed.

Figure 7

Scatter plots of the 95th percentile interaction force (A) and torque (B), as a function of variance of the orientation about the Z-direction. This is only shown for the pure translation HC tasks. (C,D) Show scatter plots for the 95th percentile interaction force and torque (FT), respectively, as a function of area of over-rotation of the orientation about the Z-direction. This is shown only for the pure rotation tasks. Of special note in these figures is the positive correlation for interaction torque and the lack of correlation for interaction force with the proposed measures of synchrony.

Figure 8

Boxplots showing the distribution of haptic interactions for each possible survey answer. (A) Shows the 95th percentile interaction force and (B) shows the 95th percentile interaction torque of each trial compared with the post-experiment survey answer of the follower. Because each dyad completed only one survey, the follower rating for that dyad was paired with the 95th percentile interaction force and torque values, giving 36 different points for each dyad. After the 95th percentile values and survey responses were paired, the boxplots were created to better visualize the distribution. The follower was asked to rate the statement “I felt there was confusion between my partner and me while moving the object” using the 5-point Likert scale. As can be noted from the graphs, the followers who strongly disagreed with the statement tended to have trials that were higher in interaction force and torque (FT) in contrast to those who agreed with the statement.

Figure 9

(A) Shows a scatter plot of the median interaction force as a function of median angular velocity. This graph shows only trials that were part of the pure rotation tasks. A strong linear negative trend is shown and thus median angular velocity generally increases as the median interaction force decreases for the pure rotation task. The size of the markers was also based on the relative completion time. Therefore, a larger marker will have a longer completion time. (B) Shows a scatter plot with the 95th percentile interaction torque as a function of median angular velocity. This graph shows only trials for the pure translation task. The data shows a positive correlation between the two metrics. A line of best fit was also included on the plot for both the haptic-only (HC) and unrestricted (UC) communication tasks. The positive trend was especially interesting since the pure translation task required no angular movement.

Figure 10

(A) shows the velocity in the Z-direction as a function of time for a single trial of the pick and place task and (B) shows the Fast Fourier Transform (FFT) of that same signal. A peak frequency of 1.49 can be seen in the graph. (C) Shows a histogram of the peak frequencies of velocity in the Z-direction for all trials. Two Peaks can be seen in the graph above: one peak below 0.33 Hz, and the other between 1.33 and 1.66 Hz.

Figure 11

Scatter plots for 95th percentile interaction force (A), 95th percentile interaction torque (B), median linear velocity (C), median angular velocity (D), and completion time (E). The X value of each point corresponds to the metric value when the dyad attempted the task with unrestricted communication (UC) and the Y value corresponds to when the dyad performed the task with haptic-only communication (HC). Thus, there were half as many points as there were trials. Blue and red markers represent an increase and decrease, respectively, in the metric when the dyad performed the same task with HC. All of the metrics had significantly different means from HC to UC at the 0.01 level except for 95th percentile interaction force.

Figure 12

Scatter plots of variance of orientation about Z for the pure translation task (A), and over-rotation about Z for the pure rotation task (B). The X value corresponds to the unrestricted communication (UC) and the Y value corresponds to the haptic-only communication (HC) trials. The blue and red markers indicate an increase and decrease, respectively, in the metric when the dyad completed the task from UC compared to HC. It should be noted in (A) that three of the four prominent red markers with high variance were all from the third repetition. If the third repetition is removed, a two-sample t-test for equal means rejects the null hypothesis at the 0.01 significance level. In (B), it should be noted that the two groups were not significantly different given the t-test above.