Mathematical computations on epidemiology: a case study of the novel coronavirus (SARS-CoV-2)

Abstract

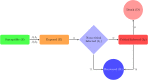
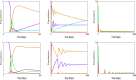
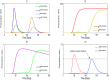
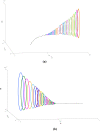
The outbreak of coronavirus COVID-19 is spreading at an unprecedented rate to the human populations and taking several thousands of life all over the world. Scientists are trying to map the pattern of the transmission of coronavirus (SARS-CoV-2). Many countries are in the phase of lockdown in the globe. In this paper we predict about the effect of coronavirus COVID-19 and give a sneak peak when it will reduce the transmission rate in the world via mathematical modelling. In this research work our study is based on extensions of the well-known susceptible-exposed-infected-recovered (SEIR) family of compartmental models and later we observe the new model changes into (SEIR) without changing its physical meanings. The stability analysis of the coronavirus depends on changing of its basic reproductive ratio. The progress rate of the virus in the critically infected cases and the recovery rate have major roles to control this epidemic. The impact of social distancing, lockdown of the country, self-isolation, home quarantine and the wariness of global public health system have significant influence on the parameters of the model system that can alter the effect of recovery rates, mortality rates and active contaminated cases with the progression of time in the real world. The prognostic ability of mathematical model is circumscribed as of the accuracy of the available data and its application to the problem.

Keywords: Bifurcation; Epidemiology; Extinction; Mathematical modelling; Persistence; Population dynamics; SARS-CoV-2.

Fig. 1

Extended SEIR model formulation

Fig. 2

Compare the simulation between the model systems (1) and (2), respectively. In the first column we illustrate the simulation of around six–seven months and in the second and third columns we consider the time about ten years. Here violet represents susceptible (S), green indicates exposed (E), orange illustrates infected (I), brown stands for recovered (R) and sky-blue is for dead (D) populations. Parameter values of system (1): ${\beta }_1=0.6,{\beta }_2=0.002,a=0.056,\alpha =0.85,{\gamma }_1=0.0025,{\gamma }_2=0.1,\mu =0.02$ and parameter values of system (2): $\mathrm{\Lambda }=0.1,\beta =0.015,a=0.017,\gamma =0.15,N=1,\mu =0.001$ (colour figure online)

Fig. 3

(i) Simulation of the model system (1) with a lockdown period correspond to the effect of before and after the lockdown. (ii) The effect of mortality rate before and after the lockdown. (iii) The effect of recovered rate before and after the lockdown. (iv) Healthcare capacity system reaches its threshold point at $I=0.1$. Parameter values of system (1): ${\beta }_1=0.6,{\beta }_2=0.002,a=0.056,\alpha =0.085,{\gamma }_1=0.0025,{\gamma }_2=0.1,\mu =0.02$. During the lockdown period ${\beta }_1$ and ${\beta }_2$ are decreased to 0.1 and 0.001, respectively, whilst other parameters are fixed. When the lockdown period is over, the value of ${\beta }_1$ is increased to 0.4 (more than lockdown period); however, ${\beta }_2$ remains unchanged as 0.001 which implies that after the lockdown is lifted people remain keep social distance with the infected populations

Fig. 4

a Hopf bifurcation diagram of system (1) with respect to the bifurcation parameter ${\gamma }_2$ is drawn in the three-dimensional space $({\gamma }_2,I_2,E)$. This figure shows that the coexistence equilibrium $E_{\ast }$ is unstable focus for ${\gamma }_2>0.16$, now system converges to stable limit cycle (depicted by different colour cycles different values of ${\gamma }_2$), stable focus for ${\gamma }_2<0.16$ (depicted by dotted line) and a Hopf bifurcation occurs at ${\gamma }_2=0.16$. b Hopf bifurcation diagram of system (1) with respect to the bifurcation parameter $\alpha$ is drawn in the three-dimensional space $(\alpha ,I_1,E)$. This figure shows that the coexistence equilibrium $E_{\ast }$ is unstable focus for $\alpha <0.5$, now system converges to stable limit cycle (depicted by different colour cycles different values of $\alpha$), stable focus for $\alpha <0.5$ (depicted by dotted line) and a Hopf-bifurcation occurs at $\alpha =0.5$. Other parameters are in the text