Modeling and Synthesis of Breast Cancer Optical Property Signatures With Generative Models
- PMID: 33684035
- PMCID: PMC8224479
- DOI: 10.1109/TMI.2021.3064464
Modeling and Synthesis of Breast Cancer Optical Property Signatures With Generative Models
Abstract
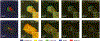
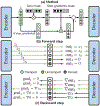
Is it possible to find deterministic relationships between optical measurements and pathophysiology in an unsupervised manner and based on data alone? Optical property quantification is a rapidly growing biomedical imaging technique for characterizing biological tissues that shows promise in a range of clinical applications, such as intraoperative breast-conserving surgery margin assessment. However, translating tissue optical properties to clinical pathology information is still a cumbersome problem due to, amongst other things, inter- and intrapatient variability, calibration, and ultimately the nonlinear behavior of light in turbid media. These challenges limit the ability of standard statistical methods to generate a simple model of pathology, requiring more advanced algorithms. We present a data-driven, nonlinear model of breast cancer pathology for real-time margin assessment of resected samples using optical properties derived from spatial frequency domain imaging data. A series of deep neural network models are employed to obtain sets of latent embeddings that relate optical data signatures to the underlying tissue pathology in a tractable manner. These self-explanatory models can translate absorption and scattering properties measured from pathology, while also being able to synthesize new data. The method was tested on a total of 70 resected breast tissue samples containing 137 regions of interest, achieving rapid optical property modeling with errors only limited by current semi-empirical models, allowing for mass sample synthesis and providing a systematic understanding of dataset properties, paving the way for deep automated margin assessment algorithms using structured light imaging or, in principle, any other optical imaging technique seeking modeling. Code is available.
Figures


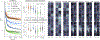
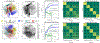



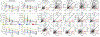
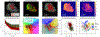

References
-
- Veronesi U, Cascinelli N, Mariani L, Greco M, Saccozzi R, Luini A et al., “Twenty-year follow-up of a randomized study comparing breast conserving surgery with radical mastectomy for early breast cancer,” N Engl J Med, vol. 347, no. 16, pp. 1227–1232, 2002. - PubMed
-
- Kaczmarski K, Wang P, Gilmore R, Overton HN, Euhus DM, Jacobs LK et al., “Surgeon Re-Excision Rates after Breast-Conserving Surgery: A Measure of Low-Value Care,” J. Am. Coll. Surg, vol. 228, no. 4, pp. 504–512, 2019. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

