Deep learning-based point-scanning super-resolution imaging
- PMID: 33686300
- PMCID: PMC8035334
- DOI: 10.1038/s41592-021-01080-z
Deep learning-based point-scanning super-resolution imaging
Abstract
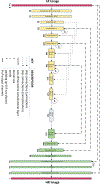
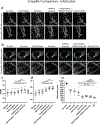
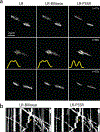
Point-scanning imaging systems are among the most widely used tools for high-resolution cellular and tissue imaging, benefiting from arbitrarily defined pixel sizes. The resolution, speed, sample preservation and signal-to-noise ratio (SNR) of point-scanning systems are difficult to optimize simultaneously. We show these limitations can be mitigated via the use of deep learning-based supersampling of undersampled images acquired on a point-scanning system, which we term point-scanning super-resolution (PSSR) imaging. We designed a 'crappifier' that computationally degrades high SNR, high-pixel resolution ground truth images to simulate low SNR, low-resolution counterparts for training PSSR models that can restore real-world undersampled images. For high spatiotemporal resolution fluorescence time-lapse data, we developed a 'multi-frame' PSSR approach that uses information in adjacent frames to improve model predictions. PSSR facilitates point-scanning image acquisition with otherwise unattainable resolution, speed and sensitivity. All the training data, models and code for PSSR are publicly available at 3DEM.org.
Conflict of interest statement
Ethics Declaration
Figures



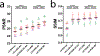








References
-
- Wang Z, Chen J & Hoi SCH Deep Learning for Image Super-resolution: A Survey. eprint arXiv:1902.06068, arXiv:1902.06068 (2019). - PubMed
-
- Jain V et al. Supervised Learning of Image Restoration with Convolutional Networks. (2007).
-
- Romano Y, Isidoro J & Milanfar P. RAISR: rapid and accurate image super resolution. IEEE Transactions on Computational Imaging 3, 110–125 (2016).
-
- Shrivastava A et al. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2107–2116.
Methods-only References
-
- Perez L & Wang J. The effectiveness of data augmentation in image classification using deep learning. arXiv preprint arXiv:1712.04621 (2017).
-
- Ronneberger O, Fischer P & Brox T in International Conference on Medical image computing and computer-assisted intervention. 234–241 (Springer; ).
-
- Shi W et al. in Proceedings of the IEEE conference on computer vision and pattern recognition. 1874–1883.
-
- Harada Y, Muramatsu S & Kiya H in 9th European Signal Processing Conference (EUSIPCO 1998). 1–4 (IEEE; ).
-
- Sugawara Y, Shiota S & Kiya H in 2018 25th IEEE International Conference on Image Processing (ICIP). 66–70 (IEEE; ).
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

