Inter-mosaic coordination of retinal receptive fields

Abstract

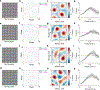
The output of the retina is organized into many detector grids, called 'mosaics', that signal different features of visual scenes to the brain^1-4. Each mosaic comprises a single type of retinal ganglion cell (RGC), whose receptive fields tile visual space. Many mosaics arise as pairs, signalling increments (ON) and decrements (OFF), respectively, of a particular visual feature⁵. Here we use a model of efficient coding⁶ to determine how such mosaic pairs should be arranged to optimize the encoding of natural scenes. We find that information is maximized when these mosaic pairs are anti-aligned, meaning that the distances between the receptive field centres across mosaics are greater than expected by chance. We tested this prediction across multiple receptive field mosaics acquired using large-scale measurements of the light responses of rat and primate RGCs. ON and OFF RGC pairs with similar feature selectivity had anti-aligned receptive field mosaics, consistent with this prediction. ON and OFF RGC types that encode distinct features have independent mosaics. These results extend efficient coding theory beyond individual cells to predict how populations of diverse types of RGC are spatially arranged.

Extended Data Figure 1 |. Anti-alignment predicted by efficient coding theory is conserved in mosaics with different densities and boundary conditions.

(a-d) Optimal spatial filters of 48 ON units and 52 OFF units, each on a 18×18 pixel grid (orange box) (a). The COMs of optimal filters forming the ON (green) and OFF (magenta) mosaics. Training was performed using a circular mask over the images to reduce edge artifacts (b). The 2-D z-scored IMCE map (c) and radial average z-scored IMCE (d) for the mosaic pairs shown in (b). (e-h) Same as in (a-d) with equal cell density (n=50) for ON and OFF mosaics. (i-l) Same as in (a-d) with number of ON and OFF units fixed at n=45 and n=55 respectively. (m-p) Same as in (a-d) with n=49 ON units and n=51 OFF units, however training was performed without a circular mask. Shaded areas are s.d.

Extended Data Figure 2 |. Mosaic coordination can persist under widely diverging RF densities.

(a, b, c) Bivariate point pattern (type 1: green, type 2: magenta) generated by modified pairwise interaction point process model (PIPP; see Methods) with interaction terms for anti-alignment (a), alignment (b) and independence (c). The density of type 2 points is four times higher than the density of type 1 points. (d, e, f) The 2-D z-scored IMCE maps corresponding to (a), (b) and (c) respectively. (g, h, i) The radial average z-scored IMCE averaged over n=100 mosaic pairs that are aligned (g), anti-aligned (h) and independent (i). Shaded areas are s.e.m.

Extended Data Figure 3 |. Mosaic coordination estimates are robust to RF subsampling.

(a) RF mosaics illustrating three different cases. ‘Measured’: no RFs are removed or added; ‘depleted’: a fraction of randomly selected RFs removed (dashed ellipses); and ‘filled’: RFs artificially added to fill mosaic gaps (thick solid ellipses). The gradient (bottom) illustrates the percentage of RFs remaining after removing or adding RFs. (b-c) The radial average z-scored IMCE is shown for different amounts of subsampling and filling of ON and OFF bt (rat) mosaics (b; blue), ON and OFF bs (rat) mosaics (b; purple), and ON and OFF parasol (primate) mosaics (c; green). bt: brisk transient, bs: brisk sustained. Each curve corresponds to an individual mosaic pair. Results are representative of n=5 retinas for ON-OFF bt, n=3 retinas for ON-OFF bs, and n=3 retinas for ON-OFF parasol RGCs. The percentage of RFs relative to measured (100%), is indicated by ‘f’. Shaded areas are s.d.

Extended Data Figure 4 |. Mosaics encoding distinct visual features appear to be independent.

(a) Example mosaics of ON and OFF brisk transient and brisk sustained RGC types. Coordination was tested across cell type (orange), and across cell type and polarity (green). (b, d, f, h) 2D z-scored IMCE map of a representative pair (left) and radial average z-scored IMCE of all pairs (right), for ONbt-ONbs (b, n=3), OFFbt-OFFbs (d, n=3), ONbt-OFFbs (f, n=3), ONbs-OFFbt (h, n=3) mosaic combinations; bt: brisk transient, bs: brisk sustained. The radial average z-scored IMCE corresponding to the 2D z-scored IMCE map (left) is shown by dashed curve. Shaded areas are s.d. (c, e, g, i) Sampling distribution from bootstrap estimates of mean coordination index for pseudo pairs (gray) and real pairs (orange/green filled circle, arrow). Number of pseudo pairs: n=12 (c), n=12 (e), n=12 (g), n=12 (i). The gray shaded region to the right of the vertical dashed line indicates value exceeding 95% confidence interval based on one-sample two-sided t-test statistic: P value = 0.33, 0.98, 0.37 and 0.46 respectively for (c), (e), (g) and (i); (n.s., not significant). Cohen’s d = 0.36, −0.006, 0.28 and −0.25 respectively for (c), (e), (g) and (i).

Extended Data Figure 5 |. Anti-alignment between ON brisk transient RF mosaics persists across light levels.

(a) RF mosaics of ON (left) and OFF (right) brisk transient RGCs, measured at photopic light level (10,000 Rh*/rod/s). The COM of RFs are indicated by black filled circles. (b-c) The 2D z-scored IMCE map (b) and radial average z-scored IMCE (right) for the mosaic pair shown in (a). (d) RF mosaics of ON (left) and OFF (right) brisk transient RGC types, at scotopic light level (1.0 R*/rod/s), from the same retina as in (a). (e-f) Same as in (b-c) for the mosaic pairs shown in (d). (g) Change in RF COMs of ON brisk transient RGCs from photopic to scotopic light level (black filled circles). Homotypic nearest-neighbor (NN) distance between RFs estimated at photopic and scotopic light levels is shown by solid and dashed red lines, respectively. (h) Distribution of fractional change in RF position of ON brisk transient RGCs across light levels expressed as a fraction of the mean NN homotypic distance at photopic light level. The smooth curve is kernel density estimate. (i-j) Same as in (g-h) for OFF brisk transient RGCs. Results are representative of n=1 retina. Shaded areas are s.d.

Figure 1:. Efficient coding predicts anti-alignment between ON and OFF RGCs with similar feature selectivity.

(a) The schematized model is trained on ~10,000 natural images to maximize the mutual information (MI) between input and collection of responses, (r₁, r₂,…, r_j) under noise and metabolic constraints (see Methods). (b) Noisy spatial filters at the beginning of training (left) become center-surround filters by end of training (right). The two learned filters exemplify ON (positive contrast) and OFF (negative contrast) RFs. Change in MI with training (center). (c) All 100 filters after optimization. Each square patch is 18×18 pixels (orange box). (d) The center of mass (filled circles) and 1 s.d. contour around the center of mass (solid line) are shown for n=46 ON-center (green) and n=54 OFF-center (magenta) filters, on the 18 × 18 pixel grid. These define the ON and OFF mosaics. (e) Center points from all ON-center (green) and OFF-center (magenta) model neurons. (f, g) 2-D z-scored IMCE map (f) and z-scored radial average IMCE (g) for the ON and OFF mosaic pairs in (e) show that the mosaics generated from the efficient coding model are anti-aligned (see Fig. 2). Shaded area is s.d.

Figure 2:. Analysis framework for measuring mosaic coordination.

(a-c) Pairs of ON (green) and OFF (magenta) mosaics generated from modified PIPP model with specific constraints on homotypic (ON-ON, OFF-OFF) and heterotypic (ON-OFF) interactions (see Methods) exhibit anti-alignment (a), alignment (b) and independence (c) respectively. Each point represents the center of mass of the spatial RF. X and Y axis units are arbitrary. Number of points for each of ON and OFF mosaic: n=50. (d) The repulsive energy between two points as a function of their separation ‘r’. The energy is set to a constant value for r≤r_min (see Eq. 3). Inset: Inverse cube repulsive force, F, and potential energy, E, between two heterotypic points (green and magenta). (e) ON mosaic (green) rigidly shifted with respect to OFF mosaic (magenta), by different amounts (length of arrow) and along different directions (direction of arrow), for estimating 2-D ‘inter-mosaic coordination energy’ (IMCE) map. (f, g, h) The 2-D z-scored IMCE maps for anti-aligned (f), aligned (g) and independent (h) mosaic pairs (n=1). X- and Y-axis have units of normalized shift. The z-scored IMCE is averaged over an annulus (shown in f) at different radial distances to obtain the radial z-scored IMCE curve. (i, j, k) An average over n=100 radial z-scored IMCE curves, each obtained by radially averaging the 2-D z-scored IMCE map for anti-aligned (i), aligned (j) and independent (k) mosaic pairs. The radial z-scored IMCE curve for the 2D z-scored IMCE map (h) is shown in blue (k). Shaded areas are s.e.m.

Figure 3:. Receptive field mosaics of functionally paired ON and OFF RGC types are anti-aligned.

(a) Representative ON (left: light blue shaded) and OFF (right: gray shaded) RF mosaics of brisk transient RGCs from rat (blue). RF contours are at 61% of peak (~1-s.d. for a Gaussian RF). Solid black circles show center-of-mass (COM). Inset: spatial RF of an individual RGC with the contour and COM. (b) The COMs of RFs of all ON (blue) and OFF (gray) brisk transient RGCs. Black contour shows region of interest (ROI) used in analysis (see Methods). (c) Left: 2-D z-scored IMCE map as a function of shift between ON and OFF brisk transient mosaics (a). Mosaic shift is normalized to the mean homotypic nearest-neighbor distance. Right: radial average z-scored IMCE. (d-f) Same as (a-c) but for ON and OFF brisk sustained RGCs (magenta). (g) RF mosaics of ON and OFF brisk transient RGCs from n=5 retinas; each column from the same retina. (h) Radial average z-scored IMCE as a function of mosaic shift for 5 mosaic pairs shown in (g). (i, j) Same as (g, h) for n=3 pairs of ON and OFF brisk sustained RGCs, each from a different retina. (k) RF mosaics of ON (top) and OFF (bottom) parasol RGCs from n=3 primate retinas (green). (l) Left: 2-D z-scored IMCE map of a representative primate retina (indicated by box in k). Right: radial average z-scored IMCE for the 3 primate retinas as a function of mosaic shift. Dashed curve corresponds to the 2D z-scored IMCE map on the left. Shaded areas are s.d.

Figure 4:. Mosaic anti-alignment is unlikely to have arisen by chance.

(a) Example mosaics of ON (left) and OFF (right) parasol RGCs, from two retinas. Mosaics from the same retina (real pairs) are indicated by red arrow; mosaics from different retinas (pseudo-pairs) are indicated by black arrow. Inset: radial average z-scored IMCE (open circles) for real (red) and pseudo (gray) mosaic pairs. Parametric fit (solid line) and area under curve (shaded region) are used to estimate coordination index (CI; see Methods). X-axis unit is normalized radial shift. (b) Sampling distribution from bootstrap estimates of mean CI for pseudo pairs (gray) and mean CI for real pairs (filled colored circles) for ON-OFF brisk transient: bt (left), and ON-OFF brisk sustained: bs (right). Number of real, pseudo pairs = 5, 40 (left); 3, 12 (right). CI mean±s.d. = 0.39±0.13 (left), 0.33±0.19 (right). The gray shaded region to the right of the vertical dashed line indicates value exceeding 95% confidence interval based on one-sample two-sided t-test statistic. (c) Same as (b) for ON-OFF parasol mosaics. Number of real, pseudo pairs = 3, 12. CI mean±s.d.=0.68±0.13. P-values and Cohen’s ds are: 3.03×10⁻⁸ and 1.61, 3.72×10⁻³ and 1.23, and 8.78×10⁻⁴⁸ and 1.19, for ON-OFF bt, ON-OFF bs and ON-OFF parasol respectively. Results are representative of n=5 retinas for ON-OFF bt (rat), n=3 retinas for ON-OFF bs (rat), and n=3 retinas for ON-OFF parasol RGC types (primate).