Sparse thalamocortical convergence

Abstract

How many thalamic neurons converge onto a cortical cell? This is an important question, because the organization of thalamocortical projections can influence the cortical architecture.^1,2 Here, we estimate the degree of thalamocortical convergence in primary visual cortex by taking advantage of the cortical expansion-neurons within a restricted volume in primary visual cortex have overlapping receptive fields driven by a smaller set of inputs from the lateral geniculate nucleus.^3-5 Under these conditions, the measurements of cortical receptive fields in a population can be used to infer the receptive fields of their geniculate inputs and the weights of their projections using non-negative matrix factorization.⁶ The analysis reveals sparse connectivity,⁷ where a handful (~2-6) of thalamic inputs account for 90% of the total synaptic weight to a cortical neuron. Together with previous findings,⁸ these results paint a picture consistent with the idea that convergence of a few inputs partly determine the retinotopy and tuning properties of cortical cells.^8-13.

Keywords: receptive fields, retinotopy, primary visual cortex, mouse, thalamocortical, connectivity, feed-forward, model, population.

Figure 1.. Measuring population receptive fields in mouse primary visual cortex.

A. The stimulus consists of flickering 2×2 checkerboards on a 10 by 18 grid covering 100 by 55 deg of the contralateral hemifield. The average response to stimulation each location is represented as an image depicting the receptive fields of the neurons. B. Examples of four (raw) receptive fields (top) and their Gaussian fits (bottom) from neurons in mouse V1.

Figure 2.. Modeling population receptive fields by non-negative matrix factorization.

A. We model the population of V1 receptive fields as a non-negative, linear combination of LGN inputs. Shaded areas represent the receptive fields of putative LGN neurons. B. The mean-squared error of the non-negative factorization falls off with the number of putative LGN inputs. In this experiment, a total of 101 receptive fields could be explained with only 18 inputs (red point). C-F. Examples of the reconstruction of V1 receptive fields from the linear combination of LGN inputs from the same population as in B. In each case, the left panels show the 1σ level-sets of the LGN receptive fields estimated by the factorization. The color code indicates the fraction of the total synaptic weight of their projections to a cortical cell. The right panels show the measured receptive fields along with its factorized representation. See also Figure S1.

Figure 3.. Sparse connectivity of thalamocortical projections.

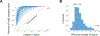
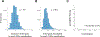
A. Fraction of total synaptic weight explained by the largest k inputs. Blue curves represent individual cells. The red curve is the average behavior across population. For each cell, the effective number of inputs is defined as the minimum number required to exceed 90% of the total input (dashed horizontal line). For reference, note that if cells had inputs with equal contributions the result would be the red, dashed line. B. Distribution of the effective number of total inputs across all neurons in all the experiments. See also Figure S1.

Figure 4.. A statistical model reconciles different estimates of the number of inputs.

By assuming a specific multivariate Dirichlet distribution of contributions we can simultaneously match the minimum number of inputs required to explain 90% of the response in the present study (A) and the number of inputs estimated by resampling (B) as done by Lien and Scanziani [7]. The distribution of contributions under such a model is a Beta distribution (C) (the marginal of the Dirichlet distribution) where small values are frequent, while large values are rare.