Joint Lp-Norm and L2,1-Norm Constrained Graph Laplacian PCA for Robust Tumor Sample Clustering and Gene Network Module Discovery
- PMID: 33708239
- PMCID: PMC7940841
- DOI: 10.3389/fgene.2021.621317
Joint Lp-Norm and L2,1-Norm Constrained Graph Laplacian PCA for Robust Tumor Sample Clustering and Gene Network Module Discovery
Abstract
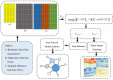
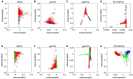
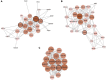
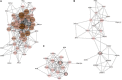
The dimensionality reduction method accompanied by different norm constraints plays an important role in mining useful information from large-scale gene expression data. In this article, a novel method named Lp-norm and L2,1-norm constrained graph Laplacian principal component analysis (PL21GPCA) based on traditional principal component analysis (PCA) is proposed for robust tumor sample clustering and gene network module discovery. Three aspects are highlighted in the PL21GPCA method. First, to degrade the high sensitivity to outliers and noise, the non-convex proximal Lp-norm (0 < p < 1)constraint is applied on the loss function. Second, to enhance the sparsity of gene expression in cancer samples, the L2,1-norm constraint is used on one of the regularization terms. Third, to retain the geometric structure of the data, we introduce the graph Laplacian regularization item to the PL21GPCA optimization model. Extensive experiments on five gene expression datasets, including one benchmark dataset, two single-cancer datasets from The Cancer Genome Atlas (TCGA), and two integrated datasets of multiple cancers from TCGA, are performed to validate the effectiveness of our method. The experimental results demonstrate that the PL21GPCA method performs better than many other methods in terms of tumor sample clustering. Additionally, this method is used to discover the gene network modules for the purpose of finding key genes that may be associated with some cancers.
Keywords: L2, 1-norm; Lp-norm; gene network modules; graph regularization; principal component analysis; sparse constraint; tumor clustering.
Copyright © 2021 Kong, Song, Liu, Zheng, Yuan, Wang and Dai.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures

References
-
- Belkin M., Niyogi P. (2002). Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 14 585–591.
-
- Belkin M., Niyogi P. (2003). Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15 1373–1396. 10.1162/089976603321780317 - DOI
-
- Bertsekas D. P. (1982). Constrained Optimization and Lagrange Multiplier Methods. Cambridge, MA: Academic Press.
LinkOut - more resources
Full Text Sources
Other Literature Sources

