Principles and practice of determining metal-protein affinities

Abstract

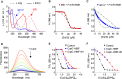
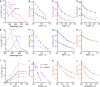
Metal ions play many critical roles in biology, as structural and catalytic cofactors, and as cell regulatory and signalling elements. The metal-protein affinity, expressed conveniently by the metal dissociation constant, KD, describes the thermodynamic strength of a metal-protein interaction and is a key parameter that can be used, for example, to understand how proteins may acquire metals in a cell and to identify dynamic elements (e.g. cofactor binding, changing metal availabilities) which regulate protein metalation in vivo. Here, we outline the fundamental principles and practical considerations that are key to the reliable quantification of metal-protein affinities. We review a selection of spectroscopic probes which can be used to determine protein affinities for essential biological transition metals (including Mn(II), Fe(II), Co(II), Ni(II), Cu(I), Cu(II) and Zn(II)) and, using selected examples, demonstrate how rational probe selection combined with prudent experimental design can be applied to determine accurate KD values.

Keywords: dissociation constant; metal probe; metalloprotein; metal–protein affinity; spectroscopic probe; transition metals.

Figure 1.. Sensitivity of probe response to measured equilibrium.

Simulated probe responses for titration of metal ions into: (a) a solution containing a metal probe P (10 µM) with K_D(P) = 5 × 10ⁿ (n = 0, ±1, ±2,…) µM; (b) a solution containing an equimolar concentration of metal probe P and competing ligand L (each 10 µM; the case 3 in Table 1) where $m=\log K_{\mathrm{D}(\mathrm{P})}/K_{\mathrm{D}(\mathrm{L})}$; (c) the same as (b) but [L] = 55 µM (the case 2 in Table 1); (d) the same as (b) but [L] = 505 µM (the case 1 in Table 1). In each case, the dashed lines mark the 20%, 50% and 80% probe responses. The probe response (PR%) at [metal]/[probe] = 1 for each titration curve with specific value n in (a) or m in (b–d) is also indicated.

Figure 2.. Examples of ‘turn-off’ probes (Mf2, quin-2 and DP peptides) and their restricted application windows.

(a–c) Determination of Zn(II)-binding stoichiometry and affinity of protein FrmRE64H in 10 mM Hepes, pH 7.0, 100 mM NaCl, 400 mM KCl: (a) solution spectra of apo- and Zn(II)-bound probe ligands quin-2 (blue traces) and Mf2 (red traces); (b) Mf2 probe response upon titration of Zn(II) ions into a solution containing Mf2 probe (10.1 µM) and FrmRE64H (18.1 µM monomer); (c) quin-2 probe response upon titration of Zn(II) ions into a solution containing quin-2 probe (13.4 µM) and FmRE64H (42.7 µM). Solid lines are curve fits to a model describing protein competition with Mf2 or quin-2 for 0.75 equivalents of Zn(II) per FrmRE64H monomer (i.e. three sites per tetramer, K_Zn1–3) generated using Dyanfit [60] (curves can also be modelled equivalently via equation 13b). Dashed lines are simulated curves with K_Zn1–3 10-fold tighter or weaker than the fitted values. Adapted from ref. [34] with data supplied by Dr. D. Osman and Prof. N.J. Robinson. (d–f) Determination of Cu(II) binding stoichiometry and affinity of protein CopC-H85F, with and without a hexa-His (6H) purification tag in 50 mM Mops pH 7.4: (d) quenching of fluorescence spectra of probe DP2 upon titration with Cu(II) ions; (e) DP2 probe response (plotted as normalised fluorescence, relative to apo-probe) upon titration of Cu(II) ions into a solution of DP2 only (4.0 µM, black); DP2 and CopC-H85F (4.0 µM each, blue); or DP2 and CopC-H85F-6H (4.0 µM each, red). (f) DP4 probe response upon titration of Cu(II) ions into a solution of DP4 only (4.0 µM, black); DP2 and CopC-H85F (4.0 µM each, blue); or DP2 and CopC-H85F-6H (4.0 µM each, red). Dashed black and blue lines in (e,f) are simple interpolation of data; solid red lines are curve fits via equation 13b to determine the weaker affinity Cu(II) site in CopC-H85F-6H (log K_D= −9.4 in (e)) and the tight-affinity Cu(II) sites in CopC-H85F and CopC-H85F-6H (indistinguishable log K_D = −14.6 in (f)). Adapted from ref. [35].

Figure 3.. Examples of the flexible application of ‘turn-on’ chromophoric probes Cu^IL₂ (L = Fs, Fz, Bca, Bcs).

(a) Solution spectra of Cu^I(Fs)₂ (magenta) and Cu^I(Fz)₂ (grey) and the respective apo-probe ligands (dashed traces). (b) Determination of Cu(I)-binding stoichiometry of CopK protein with Cu^I(Fs)₂. Change in probe concentrations (monitored by absorbance) with increasing [CopK] in a series of assay solutions (details in Table 2). The data points in triangles show the 50% values of the solid circles, demonstrating that the equilibrium position in each diluted solution has not noticeably adjusted from that present in the corresponding undiluted solution (consistent with stoichiometric binding). It was apparent that CopK could bind one equivalent of Cu(I) with sub-nM affinity. (c,d) Determination of Cu(I)-binding affinity of CopK with Cu^I(Fs)₂ (c) or Cu^I(Fz)₂ (d) (details in Table 2). The solid traces are data fits to equation 14a, deriving K_D(P) given in Table 2. The two dashed traces shows the 50% values of the filled circles and demonstrate that the equilibrium position in each diluted solution has adjusted from that present in the corresponding undiluted solution. (e) Solution spectra of Cu^I(Bca)₂ (purple) and Cu^I(Bcs)₂ (orange) (neither probe ligand has absorbance in the given visible window). (f) Determination of Cu(I)-binding stoichiometry of hGrx1 protein with the Cu^I(Bca)₂ probe (details in Table 2). It was apparent that hGrx1 could bind more than one Cu(I) with K_D(P)< 10⁻¹³ M but only one Cu(I) with K_D(P)< 10⁻¹⁴ M at pH 7.0. (g,h) Determination of Cu(I)-binding affinity of hGrx1 with Cu^I(Bca)₂ (g) or Cu^I(Bcs)₂ (h) (details in Table 2). The solid traces are the data fits to equation 14a, deriving K_D(P) given in Table 2. The dashed trace in (g) shows the 50% values of the filled circles and demonstrates that the equilibrium position in each diluted solution has adjusted from that present in the corresponding undiluted solution. (i) Cu(I) titration of each probe ligand under reducing conditions followed by absorbance at the λ_max (nm) given in (a,e): a tight turning point was observed for ligands Bcs, Bca and Fz, but not for Fs due to its relative weak affinity for Cu(I). Thus, presence of an excess of Fs is essential for its application. (j,k,l) Quantification of Cu(I)-binding to yeast Atx1 and human WLN5–6 in KPi buffer (pH 7.0): (j) determination of respective Cu(I)-binding stoichiometry with two assay solutions of Cu^I(Bca)₂ described in Table 2; determination of aM affinity of Atx1 (k) and WLN5–6 (l) with two different assay solutions of Cu^I(Bcs)₂ described in Table 2. The solid traces are the data fits to equation 14a, deriving K_D(P) given in Table 2. Data (a–d, i), (f–h) and (j–l) adapted from refs. [33], [37] and [8], respectively.

Figure 4.. Structure of selected metal probe ligands.

Structure of ML-type (fura-2, Mf2, quin-2) and ML₂-type (Par, Tar, Fs, Fz, Bca and Bcs) probe ligands, and of the fluorescent Nε-dansyl-lysine that is incorporated into each DP peptide probe (see ref. [19] for complete peptide structures).

Figure 5.. Approximate application ranges of selected spectroscopic probes for affinity determination.

Ranges of metal–protein affinities (as dissociation constants, K_D, and as free energies for metal association, ΔG, where ΔG = RT lnK_D) that may be reliably determined via competition with spectroscopic probes using typical experimental setups: For ML-type probes (fura-2, mag-fura-2, quin-2, DP1–4), ranges correspond to optimal 20–80% metal partitioning in a solution containing equimolar metal, protein and probe (e.g. 10 µM each. For Tar, range corresponds to 20–80% metal partitioning in a solution of metal (10 µM), protein (10 µM) and Tar (20 µM). For Par, range corresponds to 20–80% metal partitioning in a solution of metal (10 µM), protein (10 µM) and Par (100 µM) (excess [Par] supresses 1 : 1 complex formation; see section ‘Par’). For Fs, Fz, Bca and Bcs range corresponds to 20–80% metal partitioning in a solution of metal (30 µM), protein (30 µM) and probe (75 µM) (increasing [Cu(I)] to 30 µM enhances detection sensitivity of these probes, see Table 4). However, in practice, the application windows may be extended beyond the presented ranges by altering the experimental design (see section ‘Design and optimisation of ligand or inter-metal competition experiments’): an example is given for probe Bcs where extended bars show measurable affinity ranges for experimental setups with excess protein (200 µM, weaker limit) or excess Bcs (5 mM, tighter limit). All calculations are based on metal–probe affinities determined at pH 7.0, except those for probes DP1–4 which were determined at pH 7.4 (see Tables 3,4). The dashed line indicates that care should be taken to ensure metal speciation remains well defined where weaker probes are employed (see section ‘Non-competitive controls, medium pH and buffers’ and footnotes in Table 3); noting that weak metal–protein affinities (K_D> 10⁻⁷M) may be quantified using direct metal titration method with a careful control of the solution conditions (see section ‘Determination of metal–protein affinities via direct metal titration’).

Figure 6.. Fe(II) probes Fe^II(Tar)₂ and Fe^II(Par)₂ and their different exchange kinetics with Egta.

(a,b) Solution spectra for the probes and the probe ligands in Mops buffer (50 mM, pH 7.2, 100 mM NaCl). Inset: proposed molecular structure of a geometric isomer of the respective probe; (c) the exchange kinetics between Tar (72 µM) and Egta (220 µM) for Fe(II) (30.8 µM) in two opposite directions in a mixing cell followed by A (720 nm) for Fe^II(Tar)₂; (d) The exchange kinetics between Par (72 µM) and Egta (36 µM or 3.6 mM) for Fe(II) (30 µM) in two opposite directions in a mixing cell followed by A (705 nm) for Fe^II(Par)₂. The data were adapted from ref. [78].