Universal theory of brain waves: from linear loops to nonlinear synchronized spiking and collective brain rhythms
- PMID: 33718881
- PMCID: PMC7951957
- DOI: 10.1103/PhysRevResearch.2.023061
Universal theory of brain waves: from linear loops to nonlinear synchronized spiking and collective brain rhythms
Abstract
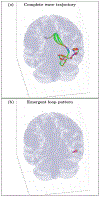
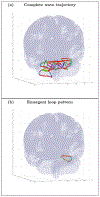
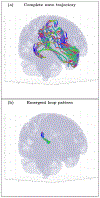
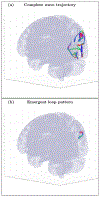
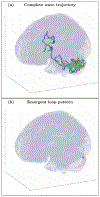
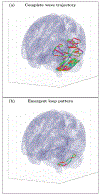
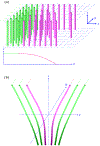
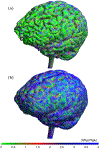
An inhomogeneous anisotropic physical model of the brain cortex is presented that predicts the emergence of non-evanescent (weakly damped) wave-like modes propagating in the thin cortex layers transverse to both the mean neural fiber direction and to the cortex spatial gradient. Although the amplitude of these modes stays below the typically observed axon spiking potential, the lifetime of these modes may significantly exceed the spiking potential inverse decay constant. Full brain numerical simulations based on parameters extracted from diffusion and structural MRI confirm the existence and extended duration of these wave modes. Contrary to the standard paradigm that the neural fibers determine the pathways for signal propagation in the brain, the signal propagation due to the cortex wave modes in highly folded areas will exhibit no apparent correlation with the fiber directions. The results are consistent with numerous recent experimental animal and human brain studies demonstrating the existence of electrostatic field activity in the form of traveling waves (including studies where neuronal connections were severed) and with wave loop induced peaks observed in EEG spectra. In addition, we demonstrate that the resonant and non-resonant terms of the nonlinear coupling between multiple modes produce both synchronous spiking-like high frequency wave activity as well as low frequency wave rhythms as a result of their unique dispersion properties. Numerical simulation of forced multiple mode dynamics shows that as forcing increases there is a transition from damped to oscillatory regime that subsequently decays away as over-excitation is reached. The resonant nonlinear coupling results in the emergence of low frequency rhythms with frequencies that are several orders of magnitude below the linear frequencies of modes taking part in the coupling. The localization and persistence of these cortical wave modes, and this new mechanism for understanding the nature of spiking behavior, have significant implications in particular for neuroimaging methods that detect electromagnetic physiological activity, such as EEG and MEG, and in general for the understanding of brain activity, including mechanisms of memory.
Figures

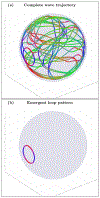
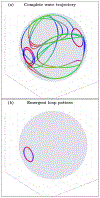
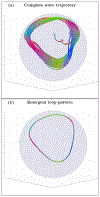



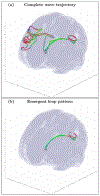








Similar articles
-
Neuronal avalanches: Sandpiles of self-organized criticality or critical dynamics of brain waves?Front Phys (Beijing). 2023 Aug;18(4):45301. doi: 10.1007/s11467-023-1273-7. Epub 2023 Mar 22. Front Phys (Beijing). 2023. PMID: 37008280 Free PMC article.
-
Brain Waves: Emergence of Localized, Persistent, Weakly Evanescent Cortical Loops.J Cogn Neurosci. 2020 Nov;32(11):2178-2202. doi: 10.1162/jocn_a_01611. Epub 2020 Jul 21. J Cogn Neurosci. 2020. PMID: 32692294 Free PMC article.
-
Collective Synchronous Spiking in a Brain Network of Coupled Nonlinear Oscillators.Phys Rev Lett. 2021 Apr 16;126(15):158102. doi: 10.1103/PhysRevLett.126.158102. Phys Rev Lett. 2021. PMID: 33929245 Free PMC article.
-
Phase correlation among rhythms present at different frequencies: spectral methods, application to microelectrode recordings from visual cortex and functional implications.Int J Psychophysiol. 1997 Jun;26(1-3):171-89. doi: 10.1016/s0167-8760(97)00763-0. Int J Psychophysiol. 1997. PMID: 9203002 Review.
-
Energetic Electron Precipitation Driven by Electromagnetic Ion Cyclotron Waves from ELFIN's Low Altitude Perspective.Space Sci Rev. 2023;219(5):37. doi: 10.1007/s11214-023-00984-w. Epub 2023 Jul 11. Space Sci Rev. 2023. PMID: 37448777 Free PMC article. Review.
Cited by
-
A dynamic generative model can extract interpretable oscillatory components from multichannel neurophysiological recordings.bioRxiv [Preprint]. 2024 Jun 10:2023.07.26.550594. doi: 10.1101/2023.07.26.550594. bioRxiv. 2024. Update in: Elife. 2024 Aug 15;13:RP97107. doi: 10.7554/eLife.97107. PMID: 37546851 Free PMC article. Updated. Preprint.
-
Imaging of brain electric field networks with spatially resolved EEG.Elife. 2025 Jun 5;13:RP100123. doi: 10.7554/eLife.100123. Elife. 2025. PMID: 40472276 Free PMC article.
-
Data-driven discovery of canonical large-scale brain dynamics.Cereb Cortex Commun. 2022 Nov 2;3(4):tgac045. doi: 10.1093/texcom/tgac045. eCollection 2022. Cereb Cortex Commun. 2022. PMID: 36479448 Free PMC article.
-
Neuronal avalanches: Sandpiles of self-organized criticality or critical dynamics of brain waves?Front Phys (Beijing). 2023 Aug;18(4):45301. doi: 10.1007/s11467-023-1273-7. Epub 2023 Mar 22. Front Phys (Beijing). 2023. PMID: 37008280 Free PMC article.
-
Critically synchronized brain waves form an effective, robust and flexible basis for human memory and learning.Sci Rep. 2023 Mar 16;13(1):4343. doi: 10.1038/s41598-023-31365-6. Sci Rep. 2023. PMID: 36928606 Free PMC article.
References
-
- Monai H, Inoue M, Miyakawa H, and Aonishi T, Low-frequency dielectric dispersion of brain tissue due to electrically long neurites, Phys Rev E Stat Nonlin Soft Matter Phys 86, 061911 (2012); - PubMed
- Ingber L and Nunez PL, Neocortical dynamics at multiple scales: EEG standing waves, statistical mechanics, and physical analogs, Math Biosci 229, 160 (2011). - PubMed
-
- Li XP, Xia Q, Qu D, Wu TC, Yang DG, Hao WD, Jiang X, and Li XM, The Dynamic Dielectric at a Brain Functional Site and an EM Wave Approach to Functional Brain Imaging, Scientific Reports 4, 6893 (2014); - PMC - PubMed
- Zalesky A, Fornito A, Cocchi L, Gollo LL, and Breakspear M, Time-resolved resting-state brain networks, Proc. Natl. Acad. Sci. U.S.A 111, 10341 (2014). - PMC - PubMed
-
- Tuch DS, Wedeen VJ, Dale AM, George JS, and Belliveau JW, Conductivity Mapping of Biological Tissue Using Diffusion MRI, Annals of the New York Academy of Sciences 888, 314 (1999); - PubMed
- Haueisen J, Tuch DS, Ramon C, Schimpf PH, Wedeen VJ, George JS, and Belliveau JW, The influence of brain tissue anisotropy on human EEG and MEG, NeuroImage 15, 159 (2002); - PubMed
- Hallez H, Vanrumste B, Hese PV, D’Asseler Y, Lemahieu I, and de Walle RV, A finite difference method with reciprocity used to incorporate anisotropy in electroencephalogram dipole source localization, Physics in Medicine & Biology 50, 3787 (2005). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
