A non-parametric method for determining epidemiological reproduction numbers

Abstract

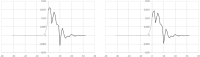
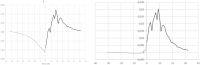
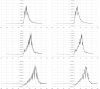
In the spreading of infectious diseases, an important number to determine is how many other people will be infected on average by anyone who has become infected themselves. This is known as the reproduction number. This paper describes a non-parametric inverse method for extracting the full transfer function of infection, of which the reproduction number is the integral. The method is demonstrated by applying it to the timeline of hospitalisation admissions for covid-19 in the Netherlands up to May 20 2020, which is publicly available from the site of the Dutch National Institute of Public Health and the Environment (rivm.nl).

Keywords: Covid-19; Estimation techniques; Infectious diseases; Reproduction number; Transmission.

Fig. 1

Left panel: the synthetic function $A(\tau )$ for cases 1 (solid line), 2 (dashed), and 3 (dash-dot). Right panel: the time series j(t) generated in case 1 (solid line), case 2 (dashed), and case 3 (dash-dot)

Fig. 2

The result of the inversion of the data j(t) shown in Fig.1, for three different values of the regularization parameter $\mu$. Left panel is case 1, right panel is case 2

Fig. 3

Determination of $A^{\prime }$ using Eq. (20) and the daily hospitalisation numbers $j(t_i)$ and cumulative numbers $C(t_i)$ : (a. left panel) with $K=0$ , (b. right panel) adjusting $K\approx 0,00993$ to obtain $A\approx 0$ for $\tau <0$. The DFT yields results in wrap around order. The plotting is done in such a way that if $A^{\prime }\ne 0$ at a positive $\tau$ , this implies that j is delayed with respect to C as would be expected. The dotted part of the curve should therefore be identical to 0, in the absence of regularization

Fig. 4

Determination of A using equation (21) with $K=0$ and the daily hospitalisation numbers $j(t_i)$ and cumulative numbers $C(t_i)$ : (a. left panel) with $K=0$ , (b. right panel) adjusting $K\approx 0,00993$ to obtain $A\approx 0$ for $\tau <0.$. The DFT yields results in wrap around order. The plotting is done in such a way that if $A\ne 0$ at a positive $\tau$, this implies that j is delayed with respect to C as would be expected

Fig. 5

Left hand panels show $A(\tau )$ with uncertainty margins under error model a, right hand panels show error model b. In all panels the grey lines provide the margins of $\pm 2,58\sigma$ around $A(\tau )$. Top row: all data up to April 2, 2020. Middle row: all data up to April 18 2020. Bottom row: all data up to May 4 2020. Note that the scale of the abscissa changes between the rows of panels