Adaptive constrained constructive optimisation for complex vascularisation processes

Abstract

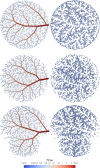
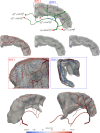
Mimicking angiogenetic processes in vascular territories acquires importance in the analysis of the multi-scale circulatory cascade and the coupling between blood flow and cell function. The present work extends, in several aspects, the Constrained Constructive Optimisation (CCO) algorithm to tackle complex automatic vascularisation tasks. The main extensions are based on the integration of adaptive optimisation criteria and multi-staged space-filling strategies which enhance the modelling capabilities of CCO for specific vascular architectures. Moreover, this vascular outgrowth can be performed either from scratch or from an existing network of vessels. Hence, the vascular territory is defined as a partition of vascular, avascular and carriage domains (the last one contains vessels but not terminals) allowing one to model complex vascular domains. In turn, the multi-staged space-filling approach allows one to delineate a sequence of biologically-inspired stages during the vascularisation process by exploiting different constraints, optimisation strategies and domain partitions stage by stage, improving the consistency with the architectural hierarchy observed in anatomical structures. With these features, the aDaptive CCO (DCCO) algorithm proposed here aims at improving the modelled network anatomy. The capabilities of the DCCO algorithm are assessed with a number of anatomically realistic scenarios.

Figure 1

Bifurcation optimisation strategy for $\mathrm{\Delta }v=6$: (left) discretised domain to look for the optimal bifurcation point $x_b$ between vessel $v_j$ and the candidate terminal point $x_i^d$; (right) new tree structure for optimal bifurcation point $x_b$ replacing vessel $v_j$ by vessels $v_{\text{p}}$, $v_{\text{s}}$ and $v_{\text{new}}$ in $\mathcal{T}$. All black dots in the left image denote the set of potential bifurcation points. Images generated with Blender v2.8 available at https://www.blender.org/.

Figure 2

Different vascular architectures obtained using the staged growth paradigm. (a) Sequential vascular growth: blue vessels correspond to a pre-defined existing vascularisation ${\mathcal{T}}_0$, while red and grey ones correspond to trees ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$, generated at stages ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$. (b) Hierarchical vascular growth: (left) vascularisation obtained with a standard CCO algorithm with parameters ${\mathcal{P}}_{\text{geo}}$ and ${\mathcal{P}}_{\text{opt}}$; (right) the first stage of the network is ${\mathcal{T}}_1$, grown in the annulus subdomain ${\mathrm{\Omega }}_1$ (light grey), while the second stage is ${\mathcal{T}}_2$, the inner circular subdomain ${\mathrm{\Omega }}_2$ (dark grey). (c) Scale-specific vascular growth: (left) vascularisation obtained with a standard CCO algorithm with $\delta =0.7$; (right) vascularisation using three stages with with $\delta =0.7$, 0.5 and 0.2 for ${\mathcal{T}}_1$ (blue vessels), ${\mathcal{T}}_2$ (grey vessels) and ${\mathcal{T}}_3$ (red vessels), respectively. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 3

Concurrent vascularisation of circular and spherical domains with equiradial vessel inlets using: (left) volumetric cost criterion (standard CCO algorithm), $\mathcal{S}=\{\mathrm{\Omega },{\mathcal{P}}_{\text{geo}},{\mathcal{P}}_{\text{opt}},\mathcal{T},1000,{\mathcal{F}}_{\text{vol}}\}$; (centre) sprouting cost criterion, $\mathcal{S}=\{\mathrm{\Omega },{\mathcal{P}}_{\text{geo}},{\mathcal{P}}_{\text{opt}},\mathcal{T},1000,{\mathcal{F}}_{\text{sprout}}\}$; (right) 2-stage multi-criteria growing with ${\mathcal{S}}_1=\{\mathrm{\Omega },{\mathcal{P}}_{\text{geo}},{\mathcal{P}}_{\text{opt}},\mathcal{T},25,{\mathcal{F}}_{\text{sprout}}\}$ and ${\mathcal{S}}_2=\{\mathrm{\Omega },{\mathcal{P}}_{\text{geo}},{\mathcal{P}}_{\text{opt}},\mathcal{T},975,{\mathcal{F}}_{\text{vol}}\}$. Parameters for central and right column cases are $c_v=0.5\times {10}^2,c_p=0.5,c_d=1.0$ and $c_v=1.0\times {10}^4,c_p=0.5,c_d=1.0$ for 2D and 3D cases, respectively, ${\mathcal{P}}_{\text{geo}}=\{\gamma =3,\delta =0\}$ and ${\mathcal{P}}_{\text{opt}}=\{\nu =1.0,f_r=0.9,f_n=8,\mathrm{\Delta }v=7\}$. Total vascular volume $F_{\text{vol}}(\mathcal{T})$ is reported below each tree. Note that ${\mathcal{F}}_{\text{sprout}}$ preserves the initial balanced conditions of inlet vessel radii, while ${\mathcal{F}}_{\text{vol}}$ tends to benefit one inlet over the other. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 4

Flow delivery using different probability distribution functions for $x_i^d$ generation: (first row) uniform distribution (standard CCO algorithm); (second row) Gaussian distribution $x_i^d\sim \mathcal{N}(\mu ,{\sigma }^2)$ with $\mu =(0,0)$ and $\sigma =(0.25,0.25)$; and (third row) Gaussian mixture of 2 distributions $x_i^d\sim 0.5\mathcal{N}({\mu }_1,{\sigma }_1^2)+0.5\mathcal{N}({\mu }_2,{\sigma }_2^2)$ with ${\mu }_1=(0,0.5)$, ${\sigma }_1=(0.25,0.25)$, ${\mu }_2=(0,-0.5)$ and ${\sigma }_2=(0.10,0.10)$. First column presents the generated tree while second column outlines the distribution of the tree terminals that are sampled from the probability distribution. The domain $\mathrm{\Omega }$ is a circle of radius 1 centred at (0, 0) with positive axes pointing towards the right and upper directions. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 5

Flow delivery in the presence of an outlet vessel $v_{\text{out}}$ with a prescribed outflow: (from left to right) tree initialisation, flow to be distributed is Q; $v_{\text{out}}$ flow is unconstrained, i.e., outlet carries the same flow than terminals inside the domain; $v_{\text{out}}$ flow is constrained to $0.5Q$; and $v_{\text{out}}$ flow is constrained to $0.99Q$. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 6

Inner retinal vasculature generated by a two-staged growth process: (first row) initialisation ${\mathcal{T}}_0$; (second row) generated tree discriminating vessels given as initial conditions (blue), generated at the stage ${\mathcal{S}}_1$ (light blue) and stage ${\mathcal{S}}_2$ (red); (third row) variation of vessel radii along the generated network. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 7

Grey matter vasculature in the superior frontal gyrus generated by a four-staged growth process: (first row) initial tree ${\mathcal{T}}_0$, illustrating the inflow and outflow constraints; (second row) from left to right, vessels corresponding to the pial network (${\mathcal{T}}_1\cup {\mathcal{T}}_2$), penetrating arterioles (${\mathcal{T}}_3$) and deep arterioles (${\mathcal{T}}_4$); (third row) superior-posterior part (left) and coronal slice at a middle section of the rostral-caudal axis (right), describing the architectural organisation of pial (red), penetrating (green) and deep (blue) vessels across the tissue; and (fourth row) final vascular tree depicting the vessel radius. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 8

Stomach vasculature generated by a five-staged growth process: (first row) initial tree ${\mathcal{T}}_0$, including the inflow and outflow constraints; (second and third rows) from left to right and top to bottom, vessels corresponding to the serosa layer (${\mathcal{T}}_1\cup {\mathcal{T}}_2$), muscularis perforators (${\mathcal{T}}_3$), mucosa layer (${\mathcal{T}}_4$) and muscularis layer (${\mathcal{T}}_5$); (bottom row) final vascular tree depicting the vessel radius from anterior and posterior views of the stomach. Images generated with ParaView version 5.4 available at https://www.paraview.org/.

Figure 9

Radius distribution of vessels generated at each stage. Each colour corresponds to a different vessel branched form the initial tree ${\mathcal{T}}_0$. Black dots in the violin indicate a sample value for the radius. First stages present a multimodal distribution in which larger radius modes correspond to vessels transporting blood to neighbour regions vascularised at another stage and smaller radius modes correspond to terminal and distribution vessels. Plots generated with Seaborn library version 0.11 available at https://seaborn.pydata.org/.

Figure 10

Comparison between standard CCO (left column) and the proposed DCCO (right column) methods. (Top) Initial vasculature; (middle) generated trees of 8000 terminal segments; (bottom) coronal slices at a middle section of the rostral-caudal axis. Images generated with ParaView version 5.4 available at https://www.paraview.org/.