Repulsive expansion dynamics in colony growth and gene expression
- PMID: 33735192
- PMCID: PMC8009408
- DOI: 10.1371/journal.pcbi.1008168
Repulsive expansion dynamics in colony growth and gene expression
Abstract
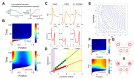
Spatial expansion of a population of cells can arise from growth of microorganisms, plant cells, and mammalian cells. It underlies normal or dysfunctional tissue development, and it can be exploited as the foundation for programming spatial patterns. This expansion is often driven by continuous growth and division of cells within a colony, which in turn pushes the peripheral cells outward. This process generates a repulsion velocity field at each location within the colony. Here we show that this process can be approximated as coarse-grained repulsive-expansion kinetics. This framework enables accurate and efficient simulation of growth and gene expression dynamics in radially symmetric colonies with homogenous z-directional distribution. It is robust even if cells are not spherical and vary in size. The simplicity of the resulting mathematical framework also greatly facilitates generation of mechanistic insights.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
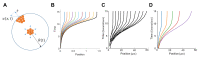


Similar articles
-
AmiC functions as an N-acetylmuramyl-l-alanine amidase necessary for cell separation and can promote autolysis in Neisseria gonorrhoeae.J Bacteriol. 2006 Oct;188(20):7211-21. doi: 10.1128/JB.00724-06. J Bacteriol. 2006. PMID: 17015660 Free PMC article.
-
A Mechanistic Collective Cell Model for Epithelial Colony Growth and Contact Inhibition.Biophys J. 2015 Oct 6;109(7):1347-57. doi: 10.1016/j.bpj.2015.08.003. Biophys J. 2015. PMID: 26445436 Free PMC article.
-
Dynamics and morphology characteristics of cell colonies with radially spreading growth fronts.Phys Rev E Stat Nonlin Soft Matter Phys. 2011 Aug;84(2 Pt 1):021917. doi: 10.1103/PhysRevE.84.021917. Epub 2011 Aug 11. Phys Rev E Stat Nonlin Soft Matter Phys. 2011. PMID: 21929029
-
Towards mechanistic models of plant organ growth.J Exp Bot. 2012 May;63(9):3325-37. doi: 10.1093/jxb/ers037. Epub 2012 Feb 27. J Exp Bot. 2012. PMID: 22371079 Review.
-
[Can mutation of the AMPD1 gene encoding human deaminase muscle muscle isozyme AMP be a prognostic marker of primary dilated cardiomyopathy?].Postepy Biochem. 1999;45(3):182-4. Postepy Biochem. 1999. PMID: 10761193 Review. Polish. No abstract available.
Cited by
-
Advances and challenges in programming pattern formation using living cells.Curr Opin Chem Biol. 2022 Jun;68:102147. doi: 10.1016/j.cbpa.2022.102147. Epub 2022 Apr 23. Curr Opin Chem Biol. 2022. PMID: 35472832 Free PMC article. Review.
-
Individual-Based Modeling of Spatial Dynamics of Chemotactic Microbial Populations.ACS Synth Biol. 2022 Nov 18;11(11):3714-3723. doi: 10.1021/acssynbio.2c00322. Epub 2022 Nov 6. ACS Synth Biol. 2022. PMID: 36336839 Free PMC article.
-
Agent-Based Modeling of Microbial Communities.ACS Synth Biol. 2022 Nov 18;11(11):3564-3574. doi: 10.1021/acssynbio.2c00411. Epub 2022 Oct 31. ACS Synth Biol. 2022. PMID: 36315012 Free PMC article. Review.
-
Navigated range expansion promotes migratory culling.Proc Natl Acad Sci U S A. 2024 Dec 10;121(50):e2408303121. doi: 10.1073/pnas.2408303121. Epub 2024 Dec 3. Proc Natl Acad Sci U S A. 2024. PMID: 39625973 Free PMC article.
References
-
- Milthorpe FL, Newton P. Studies on the expansion of the leaf surface: III. The influence of radiation on cell division and leaf expansion. Journal of Experimental Botany. 1963;14(3):483–95.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

