Dimensional engineering of a topological insulating phase in Half-Heusler LiMgAs
- PMID: 33742046
- PMCID: PMC7979736
- DOI: 10.1038/s41598-021-85806-1
Dimensional engineering of a topological insulating phase in Half-Heusler LiMgAs
Erratum in
-
Author Correction: Dimensional engineering of a topological insulating phase in Half-Heusler LiMgAs.Sci Rep. 2021 Aug 12;11(1):16739. doi: 10.1038/s41598-021-95885-9. Sci Rep. 2021. PMID: 34385523 Free PMC article. No abstract available.
Abstract
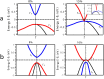
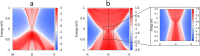
We propose a novel technique of dimensional engineering to realize low dimensional topological insulator from a trivial three dimensional parent. This is achieved by confining the bulk system to one dimension along a particular crystal direction, thus enhancing the quantum confinement effects in the system. We investigate this mechanism in the Half-Heusler compound LiMgAs with face-centered cubic (FCC) structure. At ambient conditions the bulk FCC structure exhibits a semi-conducting nature. But, under the influence of high volume expansive pressure (VEP) the system undergoes a topological phase transition (TPT) from semi-conducting to semi-metallic forming a Dirac cone. At a critical VEP we observe that, spin-orbit coupling (SOC) effects introduce a gap of [Formula: see text] 1.5 meV in the Dirac cone at high symmetry point [Formula: see text] in the Brillouin zone. This phase of bulk LiMgAs exhibits a trivial nature characterized by the [Formula: see text] invariants as (0,000). By further performing dimensional engineering, we cleave [111] plane from the bulk FCC structure and confine the system in one dimension. This low-dimensional phase of LiMgAs has structure similar to the two dimensional [Formula: see text] system. Under a relatively lower compressive strain, the low-dimensional system undergoes a TPT and exhibits a non-trivial topological nature characterized by the SOC gap of [Formula: see text] 55 meV and [Formula: see text] invariant [Formula: see text] = 1. Although both, the low-dimensional and bulk phase exhibit edge and surface states, the low-dimensional phase is far more superior and exceptional as compared to the bulk parent in terms of the velocity of Fermions ([Formula: see text]) across the surface states. Such a system has promising applications in nano-electronics.
Conflict of interest statement
The authors declare no competing interests.
Figures





Similar articles
-
Topological phase transition in the antiferromagnetic topological insulator MnBi[Formula: see text]Te[Formula: see text] from the point of view of axion-like state realization.Sci Rep. 2023 Sep 28;13(1):16343. doi: 10.1038/s41598-023-42466-7. Sci Rep. 2023. PMID: 37770454 Free PMC article.
-
Volume expansive pressure (VEP) driven non-trivial topological phase transition in LiMgBi.Phys Chem Chem Phys. 2020 Feb 28;22(8):4602-4609. doi: 10.1039/c9cp06155j. Epub 2020 Feb 13. Phys Chem Chem Phys. 2020. PMID: 32051982
-
Exploring strong and weak topological states on isostructural substitutions in TlBiSe[Formula: see text].Sci Rep. 2022 Dec 20;12(1):21970. doi: 10.1038/s41598-022-26445-y. Sci Rep. 2022. PMID: 36539475 Free PMC article.
-
Strain-induced topological magnon phase transitions: applications to kagome-lattice ferromagnets.J Phys Condens Matter. 2018 Jun 20;30(24):245803. doi: 10.1088/1361-648X/aac365. Epub 2018 May 9. J Phys Condens Matter. 2018. PMID: 29741490
-
Phase transitions, Dirac and Weyl semimetal states in Mn1-xGexBi2Te4.Sci Rep. 2025 Jan 11;15(1):1741. doi: 10.1038/s41598-024-73267-1. Sci Rep. 2025. PMID: 39799224 Free PMC article.
References
-
- Hasan MZ, Kane CL. Colloquium: topological insulators. Rev. Mod. Phys. 2010;82:3045.
-
- Fu L, Kane CL. Topological insulators with inversion symmetry. Phys. Rev. B. 2007;76:045302.
-
- Zhang H, Liu CX, Qi XL, Dai X, Fang Z, Zhang SC. Topological insulators in Bi 2 Se 3, Bi 2 Te 3 and Sb 2 Te 3 with a single Dirac cone on the surface. Nat. Phys. 2009;5:438.
-
- Kane CL, Mele EJ. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005;95:226801. - PubMed
-
- Bernevig BA, Hughes TL, Zhang SC. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science. 2006;314(5806):1757–1761. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

