Why coronavirus survives longer on impermeable than porous surfaces

Abstract

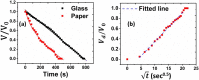
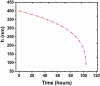
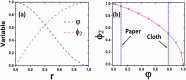
Previous studies reported that the drying time of a respiratory droplet on an impermeable surface along with a residual film left on it is correlated with the coronavirus survival time. Notably, earlier virus titer measurements revealed that the survival time is surprisingly less on porous surfaces such as paper and cloth than that on impermeable surfaces. Previous studies could not capture this distinct aspect of the porous media. We demonstrate how the mass loss of a respiratory droplet and the evaporation mechanism of a thin liquid film are modified for the porous media, which leads to a faster decay of the coronavirus on such media. While diffusion-limited evaporation governs the mass loss from the bulk droplet for the impermeable surface, a much faster capillary imbibition process dominates the mass loss for the porous material. After the bulk droplet vanishes, a thin liquid film remaining on the exposed solid area serves as a medium for the virus survival. However, the thin film evaporates much faster on porous surfaces than on impermeable surfaces. The aforesaid faster film evaporation is attributed to droplet spreading due to the capillary action between the contact line and fibers present on the porous surface and the modified effective wetted area due to the voids of porous materials, which leads to an enhanced disjoining pressure within the film, thereby accelerating the film evaporation. Therefore, the porous materials are less susceptible to virus survival. The findings have been compared with the previous virus titer measurements.

FIG. 1.

Schematic of the problem considered in the present work. The inset shows the geometry of porous fibers.

FIG. 2.

Temporal evolution of a 1 µl aqueous droplet as it evaporates on glass. Left column shows the droplet shapes at different time frames. Similar experiments were performed on plastic and stainless steel, and the results are shown in Fig. S3 of the supplementary material. Movies depicting the evaporation of the droplet on glass, plastic, and stainless steel substrates, from which the data are extracted. Multimedia view: https://doi.org/10.1063/5.0037924.1

FIG. 3.

Droplet spreading and temporal evolution of the droplet geometry on porous media. (a) Paper, side view; (b) paper, top view; and (c) cloth, top view. The red dotted circles indicate the wetted diameter of the liquid patch left after complete spreading of the droplet, i.e., when the contact angle reaches to zero. (d-i) Temporal variation of contact angle on paper and cloth. (d-ii) Temporal variation of wetted diameter on paper and cloth derived from the top views. Movies depicting the temporal variation of droplet geometry on porous surfaces, from which the data have been extracted. Multimedia view: https://doi.org/10.1063/5.0037924.2

FIG. 4.

(a) Temporal decay of normalized droplet volume for glass and paper and (b) drained volume vs square root of time plot and linear fitting for paper.

FIG. 5.

Variation of thin liquid film thickness with time on the glass substrate computed from the model.

FIG. 6.

(a) Variation of φ and ϕ₂ with r and (b) variation of surface area fraction ϕ₂ with porosity φ.

FIG. 7.

Variation of film thickness with time for (a) cloth and for (b) paper found from the model.