Stochastic Simulation of Cellular Metabolism

Abstract

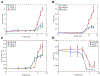
Increased technological methods have enabled the investigation of biology at nanoscale levels. Such systems require the use of computational methods to comprehend the complex interactions that occur. The dynamics of metabolic systems have been traditionally described utilizing differential equations without fully capturing the heterogeneity of biological systems. Stochastic modeling approaches have recently emerged with the capacity to incorporate the statistical properties of such systems. However, the processing of stochastic algorithms is a computationally intensive task with intrinsic limitations. Alternatively, the queueing theory approach, historically used in the evaluation of telecommunication networks, can significantly reduce the computational power required to generate simulated results while simultaneously reducing the expansion of errors. We present here the application of queueing theory to simulate stochastic metabolic networks with high efficiency. With the use of glycolysis as a well understood biological model, we demonstrate the power of the proposed modeling methods discussed herein. Furthermore, we describe the simulation and pharmacological inhibition of glycolysis to provide an example of modeling capabilities.

Keywords: Biological Modeling; Glycolysis; Metabolic Networks; Metabolomics; Ordinary Differential Equations; Queueing Theory; Stochastic Simulation.

Fig. 1.

Example Queue. Queue representing concentration C_i(t) of the metabolite M_i; μ_{i, j}, j = 1, …, L_i, are arrival rates as corresponding to processes resulting in production of metabolite M_i; μ_{i, j}, j = L_i + 1, L_i + 2, …, $K_i^{*}$, are service rates corresponding to processes using metabolite M_i. $K_i^{*}$ = number of reactions that involve metabolite M_i within the model. Additional input/output pathways are included as dashed lines to account for unknown or missing reactions. Queue adapted from Wysocki et al. 2017, Simulation of Central Glucose Metabolism Using Queueing Network, IEEE International Conference on Electro Information Technology (EIT), Lincoln, NE, 2017, pp. 217–222.

Fig. 2.

Simulated metabolic pathway from glucose to pyruvate. Arrows denote the modeled reactions. Vi, i = 0, …, 10, and V3A, V3B, are the reaction rates; for bidirectional arrows, the direction is determined by the sign of the corresponding reaction rate with the positive direction being from the top down. GLC, glucose; G6P, glucose 6-phosphate; F6P, fructose 6-phosphate; F16BP, fructose 1,6-bisphosphate; F26BP, fructose 2,6-bisphosphate; GAP glyceraldehyde 3-phosphate; DHAP, dihydroxyacetone phosphate; 13BPG, 1,3-bisphosphoglycerate; 3PG, 3-phosphoglycerate; 2PG, 2-phosphoglycerate; PEP, phosphoenolpyruvate; PYR, pyruvate.

Fig. 3.

Effect of random variability of initial concentrations of all glycolytic intermediates and kinetic constants on the simulated concentration of pyruvate. A) Means and standard deviations calculated over populations of 100 independent cells with variability applied to the concentrations of the metabolites of interest and the enzymes involved in all of the glycolysis reactions. The percent variability is derived from a zero mean Gaussian with a standard deviation of x/3 and is multiplied by the nominal concentration value. The initial concentrations of the metabolites of interest are chosen that way, and for the concentration of other enzymes involved, the operation is repeated every second, while the simulation step is 0.1 millisecond. Computation time for simulating 100 cells for 300 seconds with 0.1 millisecond time step was 36,767.18 seconds. B) Two individual cells, 10% variability of initial concentrations and 10% Gaussian noise. C) Two individual cells, 20% variability of initial concentrations and 20% Gaussian noise. D) Two individual cells, 50% variability of initial concentrations and 50% Gaussian noise.

Fig. 4.

Steady-state glycolytic flux. Metabolite concentrations were simulated with an input of 5 mM glucose over a span of 1200 seconds to model an unperturbed and constant state.

Fig. 5.

Effects of FK866 on metabolite concentrations in vitro. A) Experimental metabolomics data measuring G6P and F6P concentrations with the inhibitor FK866 in (solid blue and dashed green lines) A2780 and (red) HCT116 cancer cells, B) effects of FK866 on FBP concentrations in vitro, C) effects of FK866 on G6P and F6P concentrations in vitro, D) effects of FK866 on PEP concentrations in vitro.

Fig. 6.

Effects of GAPDH Inhibition on metabolite concentrations in silico. A) G6P and F6P, B) FBP, C) GAP and DHAP, D) PEP. In all cases, the Vmax of GAPDH was varied between 0 and 100 percent of its initial value to simulate varying levels of enzyme inhibition.