Robust data assimilation with noise: Applications to cardiac dynamics

Abstract

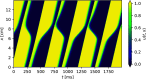
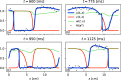
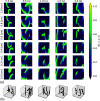
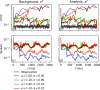
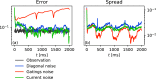
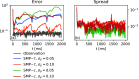
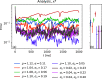
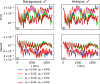
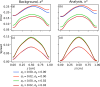
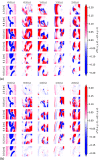
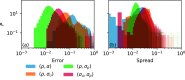
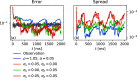
Reconstructions of excitation patterns in cardiac tissue must contend with uncertainties due to model error, observation error, and hidden state variables. The accuracy of these state reconstructions may be improved by efforts to account for each of these sources of uncertainty, in particular, through the incorporation of uncertainty in model specification and model dynamics. To this end, we introduce stochastic modeling methods in the context of ensemble-based data assimilation and state reconstruction for cardiac dynamics in one- and three-dimensional cardiac systems. We propose two classes of methods, one following the canonical stochastic differential equation formalism, and another perturbing the ensemble evolution in the parameter space of the model, which are further characterized according to the details of the models used in the ensemble. The stochastic methods are applied to a simple model of cardiac dynamics with fast-slow time-scale separation, which permits tuning the form of effective stochastic assimilation schemes based on a similar separation of dynamical time scales. We find that the selection of slow or fast time scales in the formulation of stochastic forcing terms can be understood analogously to existing ensemble inflation techniques for accounting for finite-size effects in ensemble Kalman filter methods; however, like existing inflation methods, care must be taken in choosing relevant parameters to avoid over-driving the data assimilation process. In particular, we find that a combination of stochastic processes-analogously to the combination of additive and multiplicative inflation methods-yields improvements to the assimilation error and ensemble spread over these classical methods.

FIG. 1.

Representative truth dynamics depicting $u(t,x)$ on a ring of length $14\mathrm{cm}$, exhibiting attraction to periodic alternans behavior.

FIG. 2.

Representative truth dynamics ${\mathbf{x}}^o(t)$ on a ring of length $14\mathrm{cm}$ exhibiting alternans, with observations ($\cdot$) at times $t=600,775,950,1125\mathrm{ms}$ [(a)–(d)], respectively.

FIG. 3.

(a) Dynamics of $u(t,x,y,z)$ of the 3D model truth run, sampled every $0.5\mathrm{s}$ in $t$ and $0.2\mathrm{cm}$ in $z$, and (b) scroll wave filaments at the same times throughout the domain (stretched $4\times$ in $z$ to show detail).

FIG. 4.

Comparison of the effect of classical inflation methods on 1D model assimilation results, with $\rho \in \{1.00,1.10\}$ and $\alpha \in \{0.00,0.10\}$. No stochastic inflation was used (${\sigma }_u=0$, ${\sigma }_p=0$). (a) Background and (b) analysis ensemble mean errors and (c) background and (d) analysis ensemble spreads over time.

FIG. 5.

(a) Analysis ensemble mean error and (b) analysis ensemble spread for assimilation using fixed $\rho =1$ and $\alpha =0$ (no inflation) and ${\sigma }_u=0.1$ and ${\sigma }_p=0$, i.e., SDE modeling using (8), (10), and (9) noise.

FIG. 6.

Comparison of SMP-$\tau$ (blue, orange) and SMP-$c$ (green, red) methods over time with $\rho =1$, $\alpha =0$, ${\sigma }_u=0$, and ${\sigma }_p\in \{0.05,0.10\}$, showing the (a) analysis ensemble mean error and (b) analysis ensemble spread.

FIG. 7.

Analysis ensemble mean error for optimized inflation and stochasticity parameters detailed in Table II, (a) over time and (b) temporally averaged ($\cdot$) with $y$-errorbars ($|$) denoting the standard deviation of the temporal signal.

FIG. 8.

(a) Background and (b) analysis ensemble mean errors $e_{\mathrm{RMS}}(t)$ and (c) background and (d) analysis ensemble spread ${\mathrm{sprd}}_{\mathrm{RMS}}(t)$ of assimilated sustained scroll wave turbulence over time $t$ with weak multiplicative inflation $\rho =1.01$, no additive inflation, and $({\sigma }_u,{\sigma }_p)=(0.00,0.00)$ (blue), $({\sigma }_u,{\sigma }_p)=(0.02,0.00)$ (orange), $({\sigma }_u,{\sigma }_p)=(0.00,0.02)$ (green), and $({\sigma }_u,{\sigma }_p)=(0.02,0.02)$ (red).

FIG. 9.

(a) Background and (b) analysis ensemble mean errors ${\overline{e}}_{\mathrm{RMS}}(z)$, (c) background and (d) analysis ensemble spread ${\overline{\mathrm{sprd}}}_{\mathrm{RMS}}(z)$ of assimilated sustained scroll wave turbulence over domain depth $z$ with weak multiplicative inflation $\rho =1.01$, no additive inflation, and $({\sigma }_u,{\sigma }_p)=(0.00,0.00)$ (blue), $({\sigma }_u,{\sigma }_p)=(0.02,0.00)$ (orange), $({\sigma }_u,{\sigma }_p)=(0.00,0.02)$ (green), and $({\sigma }_u,{\sigma }_p)=(0.02,0.02)$ (red).

FIG. 10.

Distribution of reconstruction error of $u^a(t,x,y,z)-u(t,x,y,z)$ of the 3D model with (a) no stochastic inflation and (b) ${\sigma }_u=0.02$ and ${\sigma }_p=0.02$, compared to the truth run, sampled every $0.5\mathrm{s}$ in $t$ and $0.2\mathrm{cm}$ in $z$. Corresponds to (a) blue and (b) red lines in Figs. 8 and 9. Compare to state dynamics in Fig. 3(a).

FIG. 11.

Normalized distribution of analysis (a) ensemble mean errors and (b) ensemble spreads according to the optimizing pairs of parameters, cases (i)–(iv) in the text.

FIG. 12.

Comparison of SDE [${\sigma }_u$, (8) noise term] and SMP (${\sigma }_p$, SMP-$\tau$) inflation in concert with multiplicative ($\rho =1.05$) and additive ($\alpha =0.05$) inflation on analysis (a) ensemble mean error and (b) ensemble spread with model error due to parametric mismatch in ${\tau }_d$, $u_c$, and $D_{||}$.

FIG. 13.

Comparison of SDE [${\sigma }_u$, (8) noise term] and SMP (${\sigma }_p$, SMP-$\tau$) inflation in concert with multiplicative ($\rho =1.05$) and additive ($\alpha =0.05$) inflation on analysis (a) ensemble mean error and (b) ensemble spread with model error due to parametric mismatch in ${\tau }_d$.