Improving reconstructive surgery design using Gaussian process surrogates to capture material behavior uncertainty
- PMID: 33756416
- PMCID: PMC8087634
- DOI: 10.1016/j.jmbbm.2021.104340
Improving reconstructive surgery design using Gaussian process surrogates to capture material behavior uncertainty
Abstract
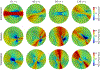
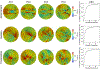
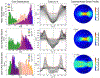
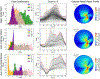
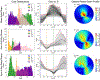
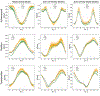
To produce functional, aesthetically natural results, reconstructive surgeries must be planned to minimize stress as excessive loads near wounds have been shown to produce pathological scarring and other complications (Gurtner et al., 2011). Presently, stress cannot easily be measured in the operating room. Consequently, surgeons rely on intuition and experience (Paul et al., 2016; Buchanan et al., 2016). Predictive computational tools are ideal candidates for surgery planning. Finite element (FE) simulations have shown promise in predicting stress fields on large skin patches and in complex cases, helping to identify potential regions of complication. Unfortunately, these simulations are computationally expensive and deterministic (Lee et al., 2018a). However, running a few, well selected FE simulations allows us to create Gaussian process (GP) surrogate models of local cutaneous flaps that are computationally efficient and able to predict stress and strain for arbitrary material parameters. Here, we create GP surrogates for the advancement, rotation, and transposition flaps. We then use the predictive capability of these surrogates to perform a global sensitivity analysis, ultimately showing that fiber direction has the most significant impact on strain field variations. We then perform an optimization to determine the optimal fiber direction for each flap for three different objectives driven by clinical guidelines (Leedy et al., 2005; Rohrer and Bhatia, 2005). While material properties are not controlled by the surgeon and are actually a source of uncertainty, the surgeon can in fact control the orientation of the flap with respect to the skin's relaxed tension lines, which are associated with the underlying fiber orientation (Borges, 1984). Therefore, fiber direction is the only material parameter that can be optimized clinically. The optimization task relies on the efficiency of the GP surrogates to calculate the expected cost of different strategies when the uncertainty of other material parameters is included. We propose optimal flap orientations for the three cost functions and that can help in reducing stress resulting from the surgery and ultimately reduce complications associated with excessive mechanical loading near wounds.
Keywords: Local flaps; Machine learning; Nonlinear finite elements; Skin biomechanics; Soft tissue mechanics.
Copyright © 2021 Elsevier Ltd. All rights reserved.
Figures


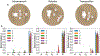
Similar articles
-
Propagation of material behavior uncertainty in a nonlinear finite element model of reconstructive surgery.Biomech Model Mechanobiol. 2018 Dec;17(6):1857-1873. doi: 10.1007/s10237-018-1061-4. Epub 2018 Aug 2. Biomech Model Mechanobiol. 2018. PMID: 30073612
-
Personalized Computational Models of Tissue-Rearrangement in the Scalp Predict the Mechanical Stress Signature of Rotation Flaps.Cleft Palate Craniofac J. 2021 Apr;58(4):438-445. doi: 10.1177/1055665620954094. Epub 2020 Sep 11. Cleft Palate Craniofac J. 2021. PMID: 32914654 Free PMC article.
-
Application of finite element modeling to optimize flap design with tissue expansion.Plast Reconstr Surg. 2014 Oct;134(4):785-792. doi: 10.1097/PRS.0000000000000553. Plast Reconstr Surg. 2014. PMID: 24945952 Free PMC article.
-
Basic flap design.Oral Maxillofac Surg Clin North Am. 2014 Aug;26(3):277-303. doi: 10.1016/j.coms.2014.05.001. Epub 2014 Jun 26. Oral Maxillofac Surg Clin North Am. 2014. PMID: 24980991 Review.
-
Flap Basics I: Rotation and Transposition Flaps.Facial Plast Surg Clin North Am. 2017 Aug;25(3):313-321. doi: 10.1016/j.fsc.2017.03.004. Epub 2017 May 30. Facial Plast Surg Clin North Am. 2017. PMID: 28676159 Review.
Cited by
-
Strain energy density as a Gaussian process and its utilization in stochastic finite element analysis: application to planar soft tissues.Comput Methods Appl Mech Eng. 2023 Feb 1;404:115812. doi: 10.1016/j.cma.2022.115812. Epub 2022 Dec 10. Comput Methods Appl Mech Eng. 2023. PMID: 37235184 Free PMC article.
-
On modeling the multiscale mechanobiology of soft tissues: Challenges and progress.Biophys Rev (Melville). 2022 Aug 15;3(3):031303. doi: 10.1063/5.0085025. eCollection 2022 Sep. Biophys Rev (Melville). 2022. PMID: 38505274 Free PMC article. Review.
-
Bayesian Inference With Gaussian Process Surrogates to Characterize Anisotropic Mechanical Properties of Skin From Suction Tests.J Biomech Eng. 2022 Dec 1;144(12):121003. doi: 10.1115/1.4054929. J Biomech Eng. 2022. PMID: 35788269 Free PMC article.
-
Analysis of In Vivo Skin Anisotropy Using Elastic Wave Measurements and Bayesian Modelling.Ann Biomed Eng. 2023 Aug;51(8):1781-1794. doi: 10.1007/s10439-023-03185-2. Epub 2023 Apr 6. Ann Biomed Eng. 2023. PMID: 37022652 Free PMC article.
-
Generative Hyperelasticity with Physics-Informed Probabilistic Diffusion Fields.Eng Comput. 2025 Feb;41(1):51-69. doi: 10.1007/s00366-024-01984-2. Epub 2024 May 18. Eng Comput. 2025. PMID: 40330696
References
-
- Gurtner GC, Dauskardt RH, Wong VW, Bhatt KA, Wu K, Vial IN, Padois K, Korman JM, Longaker MT, Improving cutaneous scar formation by controlling the mechanical environment: large animal and phase i studies, Annals of surgery 254 (2011) 217–225. - PubMed
-
- Buchanan PJ, Kung TA, Cederna PS, Evidence-based medicine: wound closure, Plastic and reconstructive surgery 138 (2016) 257S–270S. - PubMed
-
- Lee T, Turin SY, Gosain AK, Bilionis I, Tepole AB, Propagation of material behavior uncertainty in a nonlinear finite element model of reconstructive surgery, Biomechanics and modeling in mechanobiology 17 (2018) 1857–1873. - PubMed
-
- Leedy JE, Janis JE, Rohrich RJ, Reconstruction of acquired scalp defects: an algorithmic approach, Plastic and reconstructive surgery 116 (2005) 54e–72e. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

