Virus transport from drywells under constant head conditions: A modeling study

Abstract

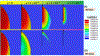
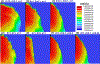
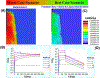
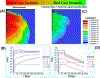
Many arid and semi-arid regions of the world face challenges in maintaining the water quantity and quality needs of growing populations. A drywell is an engineered vadose zone infiltration device widely used for stormwater capture and managed aquifer recharge. To our knowledge, no prior studies have quantitatively examined virus transport from a drywell, especially in the presence of subsurface heterogeneity. Axisymmetric numerical experiments were conducted to systematically study virus fate from a drywell for various virus removal and subsurface heterogeneity scenarios under steady-state flow conditions from a constant head reservoir. Subsurface domains were homogeneous or had stochastic heterogeneity with selected standard deviation (σ) of lognormal distribution in saturated hydraulic conductivity and horizontal (X) and vertical (Z) correlation lengths. Low levels of virus concentration tailing can occur even at a separation distance of 22 m from the bottom of the drywell, and 6-log₁₀ virus removal was not achieved when a small detachment rate (k_d1=1 × 10⁻⁵ min⁻¹) is present in a homogeneous domain. Improved virus removal was achieved at a depth of 22 m in the presence of horizontal lenses (e.g., X=10 m, Z=0.1 m, σ=1) that enhanced the lateral movement and distribution of the virus. In contrast, faster downward movement of the virus with an early arrival time at a depth of 22 m occurred when considering a vertical correlation in permeability (X=1 m, Z=2 m, σ=1). Therefore, the general assumption of a 1.5-12 m separation distance to protect water quality may not be adequate in some instances, and site-specific microbial risk assessment is essential to minimize risk. Microbial water quality can potentially be improved by using an in situ soil treatment with iron oxides to increase irreversible attachment and solid-phase inactivation.

Keywords: Drywell; HYDRUS (2D/3D); Managed aquifer recharge; Vadose zone; Virus; Water Quality.

Fig. 1.

The drywell geometry, dimensions, initial condition, the boundary conditions, and the X and $Z$-correlation length scales (virus BTC sampling location depth corresponding to the Z-axis) for the 2D-axisymmetrical flow domain for the water flow and solute transport. The detailed drywell geometry and the water flow dynamics were presented in our previous study (Sasidharan et al., 2018a).

Fig. 2.

The schematic of various virus removal processes during transport in porous media that were applied in the numerical experiments presented in this study.

Fig. 3.

The virus removal (log scale) for the irreversible attachment scenario at various sticking efficiencies ($\mathrm{\alpha }$)=0, 1×10⁻⁵, 1×10⁻⁴, and 1×10⁻³ when detachment coefficient ($k_d$)=0 in a homogeneous domain (Fort Irwin Soil) after 90 days of a continuous pulse of virus (A) and the 365^th day of steady-state virus-free water flow (B).

Fig. 4.

The virus breakthrough curve (log scale) for the irreversible attachment scenario when sticking efficiency ($\mathrm{\alpha }$)=0 (A), 1×10⁻⁵ (B), 1×10⁻⁴ (C), and 1×10⁻³ (D) at depths=1, 4, 6, 13, and 22 m when the detachment coefficient ($k_d$)=0 in a homogeneous domain (Fort Irwin Soil) over 365 days (90 days of a continuous pulse of virus and 275-days of steady-state virus-free water flow) simulation.

Fig. 5.

The virus breakthrough curve (log scale) at depths=1, 4, 6, 13, and 22 m for the detachment (A), liquid inactivation (B), solid-phase inactivation (C), reversible fraction (D), reversible fraction+${\mu }_s$ (E), and reversible fraction+${\mu }_s+{\mu }_l$ (F) scenarios. The Irreversible attachment scenario is presented as the doted (brown) line. The 6-log₁₀ removal is shown as the dashed blue line. Table 1 (Set I and Set II) shows the corresponding virus removal parameters.

Fig. 6.

The virus concentration distribution profile (log scale) for heterogeneous $X$=10, $Z$=0.1, $\sigma$=1 (horizontal lens) (A), $X$=1, $Z$=0.1, $\sigma$=1 (B), $X$=0.1, $Z$=0.1, $\sigma$=1 (C), $X$=1, $Z$=1, $\sigma$=1 (D), $X$=1, $Z$=2, $\sigma$=1 (thick vertical lens) (E), $X$=1, $Z$=0.1, $\sigma$=0.5 (F), and $X$=1, $Z$=0.1, $\sigma$=0.25 (G)) Fort Irwin soil flow domains at 365 day after 90 days of a continuous pulse of virus transport and 275-days of steady-state water flow simulation for detachment scenario.

Fig. 7.

The virus concentration distribution for the worst-case (detachment) (A) and best-case (reversible fraction + ${\mu }_s+{\mu }_l$) (C) removal scenarios in the “$X$=1, $Z$=2, and $\sigma$=1” flow domain. The virus breakthrough curve at depths=1, 4, 6, 13, and 22 m in the “$X$=1, $Z$=2, and $\sigma$=1” flow domain for the worst-case (B) and best-case (D) removal scenarios.

Fig. 8.

The virus concentration distribution for the worst-case (detachment) (A) and best case (reversible fraction + ${\mu }_s+{\mu }_l$) (C) removal scenarios in the “$X$=10, $Z$=0.1, and $\sigma$=1” flow domain. The virus breakthrough curve at depths=1, 4, 6, 13, and 22 m in the “$X$=10, $Z$=0.1, and $\sigma$=1” flow domain for the worst-case (B) and best-case (D) removal scenarios.

Fig. 9.

The virus breakthrough curves for the worst-case (detachment) removal scenario at 22 m as a function of time during 30 days (A) and 365 days (B). The virus breakthrough curves for the best-case (reversible fraction + ${\mu }_s+{\mu }_l$) removal scenario at 22 m as a function of time during 15 days (C) and 365 days (D).