Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Mar 29;16(3):e0248861.
doi: 10.1371/journal.pone.0248861. eCollection 2021.

A protein structural study based on the centrality analysis of protein sequence feature networks

Xiaogeng Wan  1 , Xinying Tan  2
Affiliations

A protein structural study based on the centrality analysis of protein sequence feature networks

Xiaogeng Wan et al. PLoS One. .

Abstract

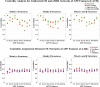
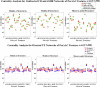
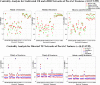
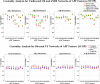
In this paper, we use network approaches to analyze the relations between protein sequence features for the top hierarchical classes of CATH and SCOP. We use fundamental connectivity measures such as correlation (CR), normalized mutual information rate (nMIR), and transfer entropy (TE) to analyze the pairwise-relationships between the protein sequence features, and use centrality measures to analyze weighted networks constructed from the relationship matrices. In the centrality analysis, we find both commonalities and differences between the different protein 3D structural classes. Results show that all top hierarchical classes of CATH and SCOP present strong non-deterministic interactions for the composition and arrangement features of Cystine (C), Methionine (M), Tryptophan (W), and also for the arrangement features of Histidine (H). The different protein 3D structural classes present different preferences in terms of their centrality distributions and significant features.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Centrality analysis for the networks of N features (CATH).
This figure shows the centrality results for the networks of N features (CATH data). The normalized centralities are plotted against the features (represented by the amino acid abbreviations). In the CR and nMIR networks, the red curves represent the degree centralities, while the green curves represent the eigenvector centralities. In the TE networks, the red curves present the in and out degree centralities, the blue and black curves represent the Katz and PageRank centralities.
Fig 2
Fig 2
Centrality analysis for the networks of N features (SCOP). This figure shows the centrality results for the networks of the N features (SCOP data).
Fig 3
Fig 3. Centrality analysis for the networks of μ features (CATH).
This figure shows the centrality results for the networks of μ features (CATH data).
Fig 4
Fig 4. Centrality analysis for the networks of μ features (SCOP).
This figure shows the centrality results for the networks of μ features (SCOP data).
Fig 5
Fig 5. Centrality analysis for the networks of D features (CATH).
This figure shows the centrality results for the networks of D features (CATH data).
Fig 6
Fig 6. Centrality analysis for the networks of D features (SCOP).
This figure shows the centrality results for the networks of D features (SCOP data).
Fig 7
Fig 7. Centrality analysis for the networks of APF features (CATH).
This figure shows the centrality results for the networks of APF features (CATH data). The normalized centralities are plotted against the features (represented by the indices of the properties as listed in S2 Table).
Fig 8
Fig 8. Centrality analysis for the networks of APF features (SCOP).
This figure shows the centrality results for the networks of APF features (SCOP data).
Fig 9
Fig 9. Centrality analysis for the networks of PseAAC features with λ = 0 (CATH).
This figure shows the centrality results for the undirected CR and nMIR networks (upper plots) and the directed TE networks (bottom plots) for the PseAAC features with λ = 0 (CATH data).
Fig 10
Fig 10. Centrality analysis for the networks of PseAAC features with λ = 0 (SCOP).
This figure shows the centrality results for the undirected CR and nMIR networks (upper plots) and the directed TE networks (bottom plots) for the PseAAC features with λ = 0 (SCOP data).
Fig 11
Fig 11. Centrality analysis for the networks of PseAAC features with λ = 10 (CATH).
This figure shows the centrality results for the networks of PseAAC features with λ = 10 (CATH data). The normalized centralities are plotted against the features (represented by the amino acid abbreviations and the indices of the λ-tier correlations).
Fig 12
Fig 12. Centrality analysis for the networks of PseAAC features with λ = 10 (SCOP).
This figure shows the centrality results for the networks of PseAAC features with λ = 10 (SCOP data).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Wang J, Wang Z, Tian X. Bioinformatics: Fundementals and applications. Tsinghua University Press. 2014.
    1. Levitt M. Nature of the protein universe. Proceedings of the National Academy of Sciences of the United States of America. 2009; 106 (27): 11079–11084. 10.1073/pnas.0905029106 - DOI - PMC - PubMed
    1. Yau SS-T, Yu C, He RL. A protein map and its application. DNA and Cell Biology. 2008; 27: 241–250. 10.1089/dna.2007.0676 - DOI - PubMed
    1. Yu C, Cheng SY, He RL, Yau SS-T. Protein map: An alignment-free sequence comparison method based on various properties of amino acids. Gene. 2011; 486(1–2): 110–118. 10.1016/j.gene.2011.07.002 - DOI - PubMed
    1. Yu C, Deng M, Cheng SY, Yau SC, He RL, Yau SS-T. Protein space: A natural method for realizing the nature of protein universe. Journal of Theoretical Biology. 2013; 318: 197–204. 10.1016/j.jtbi.2012.11.005 - DOI - PubMed

LinkOut - more resources