Laser cooling of antihydrogen atoms

Abstract

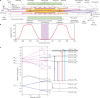
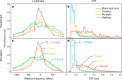
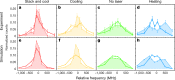
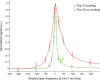
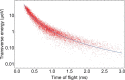
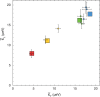
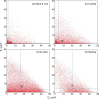
The photon-the quantum excitation of the electromagnetic field-is massless but carries momentum. A photon can therefore exert a force on an object upon collision¹. Slowing the translational motion of atoms and ions by application of such a force^2,3, known as laser cooling, was first demonstrated 40 years ago^4,5. It revolutionized atomic physics over the following decades^6-8, and it is now a workhorse in many fields, including studies on quantum degenerate gases, quantum information, atomic clocks and tests of fundamental physics. However, this technique has not yet been applied to antimatter. Here we demonstrate laser cooling of antihydrogen⁹, the antimatter atom consisting of an antiproton and a positron. By exciting the 1S-2P transition in antihydrogen with pulsed, narrow-linewidth, Lyman-α laser radiation^10,11, we Doppler-cool a sample of magnetically trapped antihydrogen. Although we apply laser cooling in only one dimension, the trap couples the longitudinal and transverse motions of the anti-atoms, leading to cooling in all three dimensions. We observe a reduction in the median transverse energy by more than an order of magnitude-with a substantial fraction of the anti-atoms attaining submicroelectronvolt transverse kinetic energies. We also report the observation of the laser-driven 1S-2S transition in samples of laser-cooled antihydrogen atoms. The observed spectral line is approximately four times narrower than that obtained without laser cooling. The demonstration of laser cooling and its immediate application has far-reaching implications for antimatter studies. A more localized, denser and colder sample of antihydrogen will drastically improve spectroscopic^11-13 and gravitational¹⁴ studies of antihydrogen in ongoing experiments. Furthermore, the demonstrated ability to manipulate the motion of antimatter atoms by laser light will potentially provide ground-breaking opportunities for future experiments, such as anti-atomic fountains, anti-atom interferometry and the creation of antimatter molecules.

Fig. 1. The ALPHA-2 apparatus schematic and antihydrogen energy levels.

a, Central parts of the ALPHA-2 apparatus are schematically shown. The field for the magnetic minimum trap is produced by five mirror coils for longitudinal confinement and one octupole coil for transverse confinement. The trap has a depth of about 50 μeV with an axial length of 280 mm and a diameter of 44.35 mm. The magnetic trap is superimposed on a cryogenic Penning trap (the electrodes are shown in yellow). An external solenoid, not shown, provides a 1-T base field for charged particle trapping and cooling. The solenoids at either end of the trap further boost the field in the preparation traps to 3 T for more efficient cyclotron cooling of electrons, positrons (e⁺) and antiprotons ($\overline{p}$), before antihydrogen synthesis. The atom trap is surrounded by a silicon vertex annihilation detector made of three layers of double-sided microstrip sensors. The pulsed Lyman-α light at 121.6 nm, generated in a gas cell immediately outside the ultrahigh vacuum chamber, is introduced through a magnesium fluoride window with an angle of 2.3° with respect to the trap axis to allow particle loading on axis into the Penning trap. The intensity of the 121.6-nm pulse is recorded by a solar-blind photomultiplier (PMT) placed after the trap. A cryogenic optical cavity serves to both build up the 243.1-nm laser light needed to drive the 1S–2S transitions, and to provide the counter-propagating photons that cancel the first-order Doppler shift. Microwaves, used to drive hyperfine transitions, and to perform electron cyclotron resonance magnetometry, are injected through the microwave guide. According to the coordinate system shown, we define the longitudinal kinetic energy to be 1/2m_H$v_z^2$, and the transverse one to be 1/2m_H $\left({v_x}^2+{v_y}^2\right)$, where m_H is the mass of antihydrogen, and v_x, v_y and v_z are the velocity components in the x, y and z directions. b, Magnetic field profile on the axis of the trap. The shaded region illustrates a volume in which the field on axis is uniform to 0.01 T, corresponding to a Zeeman shift of 140 MHz in the 1S–2P_a transition. Immediately before reach run, the magnetic field at the centre of the trap was measured via electron cyclotron resonance and the laser frequencies were adjusted accordingly. The measured magnetic minimum field, averaged over the pre-run measurements, was 1.03270 ± 0.00007 T, where the error is the standard deviation from the set of measurements. c, The energy levels of the antihydrogen in the n = 1 and n = 2 states are depicted as a function of the magnetic field. On the vertical axis, the centroid energy difference, E_1S–2S = 2.4661 × 10¹⁵ Hz, has been suppressed. The dotted vertical black line represents the field at the magnetic minimum of our trap, 1.0327 T (see above). Details of the energy levels near this field and their state labels are shown on the right of the figure. The first value in the ket notation represents the quantum number of the projection of the total angular momentum of the positron, m_L + m_S, where L is the orbital angular momentum (L = 0 for the S state and L = 1 for the P state, respectively) and S is the spin (S = 1/2). The double arrow shows the antiproton spin (up or down). Initially, both the 1S_c and 1S_d states are trapped in our magnetic trap. The grey arrow indicates the microwave-driven 1S_c → 1S_b transition to eliminate the anti-atoms in the 1S_c hyperfine state and prepare a doubly spin-polarized antihydrogen sample in the 1S_d state. The solid and broken red (cyan) arrows indicate the cycling transition for laser cooling (heating) with red (blue) detuning −δ (+δ′). The purple arrow represents the probe laser excitation to the 2P_c– level. Note that the 2P_c state at a magnetic field of about 1 T is a superposition of the positron spin-up (m_L = 0, m_S = +1/2) and spin-down (m_L = +1, m_S = –1/2) states. Owing to this superposition, upon de-excitation from the 2P_c state, the anti-atom can either go back to the original 1S_d state, or undergo an effective ‘spin flip’ transition to the 1S_a state. In the latter case, the anti-atom is forced out of the trap and detected via its annihilation signal. The black arrows show the two-photon excitation from the 1S_d state to the 2S_d state.

Fig. 2. Laser cooling of antihydrogen.

The spectral lineshapes and the TOF distributions, obtained during the probing phase by detecting antihydrogen annihilations resulting from laser-induced spin flips. In all cases, the curves are drawn to guide the eye. a, The experimental lineshapes given by the number of annihilation counts within a TOF time window of 0 to 3 ms, as a function of the probe laser frequency relative to the resonant frequency. b, TOF distributions representing the time between the nanosecond-scale probe laser pulse and the detection of the annihilation. Events with an axial annihilation position between +10 cm and –10 cm are plotted. The distributions are compared for the experimental series given in Table 1: the no-laser series (green); the heating series with a detuning of approximately +160 MHz (blue); the cooling series with a –240-MHz detuning (orange); and the ‘stack and cool’ series where a –230-MHz detuning was applied during both the stacking phase and the cooling phase (red). c, d, The corresponding simulations for the lineshapes (c) and the TOF distributions (d). Each distribution is normalized to its total number of counts, and the error bars represent 1 s.d. counting statistical uncertainties. The values labelled ${\overline{E}}_{\mathrm{L}}$ and ${\overline{E}}_{\mathrm{T}}$ represent the mean of ‘true’ longitudinal and transverse energies, respectively, of the simulated atoms at the time of the spin-flip transitions. See text and Methods.

Fig. 3. Reconstructed transverse energies of the laser-cooled and heated antihydrogen.

a, Distributions of the transverse kinetic energies reconstructed from the TOF of antihydrogen for different series. On the horizontal axis, the mean values of the reconstructed energies for each series are marked by downward-facing arrows, and the medians by upward-facing arrows. b, Corresponding simulations, where simulated events are analysed in the same way as above. The error bars represent 1 s.d. statistical uncertainties. See text and Methods.

Fig. 4. Comparison of spectral lineshapes between transversely cold and hot anti-atoms within the same series in the cooling experiment.

a, Comparison of the spectral lineshapes between equally sized subsamples of the ‘stack and cool’ series data. The lineshape for the subsample with the transverse energy greater (smaller) than its median value is shown with a solid line (dashed line filled under the curve). b–h, Analogous comparisons are given for the cooling (b), no-laser (c) and heating (d) series, and the corresponding simulations (e–h). The error bars represent 1 s.d. counting statistics. In all cases, the curves are drawn to guide the eye. These correlations indicate that in the laser-cooling series (a, b), transversely colder atoms are also longitudinally colder, while the correlation is reversed for the heating series (d). See text and Methods.

Fig. 5. Recorded spectra of the 1S–2S transition from runs A and B.

The fits use lineshapes informed by simulation (Methods). Both of the spectra are normalized to their fitted height and have a frequency-independent background subtracted to illustrate the difference in line shape. The subtracted background is 3.6 (18.3) annihilation events per bin in run A (B) and the fitted signal amplitude is 84.6 (135) events. The error bars represent 1 s.d. counting statistics. a.u., arbitrary units.

Extended Data Fig. 1. Comparison of the reconstructed and true transverse energies in simulated events.

Each red point shows a simulated antihydrogen’s true transverse energy at the time of the spin flip, plotted against its TOF. The simulation was performed for the conditions of the ‘stack and cool’ series. The true energies can be compared with the reconstructed transverse energies (blue curve), derived from the TOF using the one-dimensional model. The mean of the true energies agrees to within 10% with that of the reconstructed energies. See Methods.

Extended Data Fig. 2. Sample-by-sample correlations between the longitudinal and transverse motions of antihydrogen in the cooling experiment.

The correlations between the longitudinal and the transverse energies, as represented by the parameters ${\widetilde{ϵ}}_{\mathrm{L}}$ and ${\overline{ϵ}}_{\mathrm{T}}$, are shown for the eight experimental runs (circles with error bars). The corresponding simulations for four series (squares) are also shown, for which the simulated data are analysed in the same way as the experimental data. ${\widetilde{ϵ}}_{\mathrm{L}}$ is an estimated upper limit on the average longitudinal kinetic energy of the sample and ${\overline{ϵ}}_{\mathrm{T}}$ is the mean of the reconstructed transverse kinetic energies given in Fig. 3a, b. See Fig. 2 for the colour code for the series. The error bars represent 1 s.d. statistical uncertainties. These correlations corroborate the observation that antihydrogen atoms are cooled in both longitudinal and transverse degrees of freedom.

Extended Data Fig. 3. Simulated correlations between the longitudinal and transverse energies within the same samples in the cooling experiment.

a–d, Red dots show the values of true longitudinal (E_L) and transverse (E_T) energies of simulated antihydrogen atoms at the time of spin flip, for the four different series. The blue dashed lines depict the median longitudinal and transverse energies (cf. Fig. 4) and the black crosses indicate their mean values. Note the appearance of an intense peak near E_L and E_T ≈ 0, in the ‘stack and cool’ (a) and cooling (b) series, compared with the no-laser series (c), indicating strong three-dimensional cooling. The distributions show that the total energy, E_L + E_T is bound by the trap depth of about 50 μeV. This results in anti-correlation between E_L and E_T for the atoms with a total energy comparable to the trap depth. This anti-correlation is enhanced in the heating series (d), where the population of the coldest atoms (near E_L and E_T ≈ 0) are removed by the laser heating. These features in the simulated events qualitatively explain the observations in Fig. 4.