Revising Berg-Purcell for finite receptor kinetics

Abstract

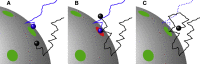
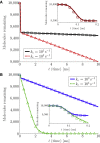
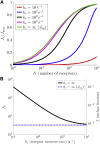
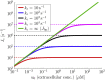
From nutrient uptake to chemoreception to synaptic transmission, many systems in cell biology depend on molecules diffusing and binding to membrane receptors. Mathematical analysis of such systems often neglects the fact that receptors process molecules at finite kinetic rates. A key example is the celebrated formula of Berg and Purcell for the rate that cell surface receptors capture extracellular molecules. Indeed, this influential result is only valid if receptors transport molecules through the cell wall at a rate much faster than molecules arrive at receptors. From a mathematical perspective, ignoring receptor kinetics is convenient because it makes the diffusing molecules independent. In contrast, including receptor kinetics introduces correlations between the diffusing molecules because, for example, bound receptors may be temporarily blocked from binding additional molecules. In this work, we present a modeling framework for coupling bulk diffusion to surface receptors with finite kinetic rates. The framework uses boundary homogenization to couple the diffusion equation to nonlinear ordinary differential equations on the boundary. We use this framework to derive an explicit formula for the cellular uptake rate and show that the analysis of Berg and Purcell significantly overestimates uptake in some typical biophysical scenarios. We confirm our analysis by numerical simulations of a many-particle stochastic system.

Figure 1

(a) The blue and black molecules compete to bind to a surface receptor. (b) The blue molecule binds to a receptor. The black molecule is then temporarily blocked from binding to that receptor. (c) After some time, the blue molecule is absorbed by the receptor, and that receptor is free to bind the black molecule. To see this figure in color, go online.

Figure 2

Comparison of stochastic simulations (squares and triangles) to the deterministic PDE-ODE system (solid and dotted curves) for the cylindrical domain for different values of the receptor turnover rate k_c. The insets zoom in at early times. See the text for details. To see this figure in color, go online.

Figure 3

(a) Cellular uptake as a function of the number of cell surface receptors for different turnover rates k_c. (b) Number of receptors needed so that J^_∗ = J_bp (N^_∗ in Eq. 42) on the left axis as a function of k_c. The right axis gives the corresponding fraction of the cell surface covered by receptors (f in Eq. 44). See Table 1 for parameter values. To see this figure in color, go online.

Figure 4

Cellular uptake as a function of the extracellular concentration for different turnover rates k_c. The dashed horizontal lines are the maximal uptake rates for different turnover rates. See Table 1 for parameter values. To see this figure in color, go online.

Figure 5

Cellular uptake as a function of the extracellular concentration for different turnover rates k_c, with breakup rate k_b = 0 in (a) and k_b = 10k_c in (b). The solid curves correspond to J^_∗ in Eqs. 23 and 24, and the dotted curves correspond to J_mm in Eq. 46. See Table 1 for other parameter values. To see this figure in color, go online.