Modelling the early phase of the Belgian COVID-19 epidemic using a stochastic compartmental model and studying its implied future trajectories

Abstract

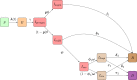
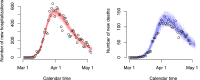
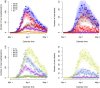
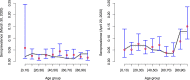
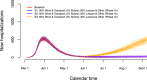
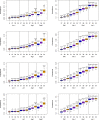
Following the onset of the ongoing COVID-19 pandemic throughout the world, a large fraction of the global population is or has been under strict measures of physical distancing and quarantine, with many countries being in partial or full lockdown. These measures are imposed in order to reduce the spread of the disease and to lift the pressure on healthcare systems. Estimating the impact of such interventions as well as monitoring the gradual relaxing of these stringent measures is quintessential to understand how resurgence of the COVID-19 epidemic can be controlled for in the future. In this paper we use a stochastic age-structured discrete time compartmental model to describe the transmission of COVID-19 in Belgium. Our model explicitly accounts for age-structure by integrating data on social contacts to (i) assess the impact of the lockdown as implemented on March 13, 2020 on the number of new hospitalizations in Belgium; (ii) conduct a scenario analysis estimating the impact of possible exit strategies on potential future COVID-19 waves. More specifically, the aforementioned model is fitted to hospital admission data, data on the daily number of COVID-19 deaths and serial serological survey data informing the (sero)prevalence of the disease in the population while relying on a Bayesian MCMC approach. Our age-structured stochastic model describes the observed outbreak data well, both in terms of hospitalizations as well as COVID-19 related deaths in the Belgian population. Despite an extensive exploration of various projections for the future course of the epidemic, based on the impact of adherence to measures of physical distancing and a potential increase in contacts as a result of the relaxation of the stringent lockdown measures, a lot of uncertainty remains about the evolution of the epidemic in the next months.

Keywords: Age-structured compartmental SEIR model; Hospitalization and mortality data; Markov Chain Monte Carlo (MCMC); Serial serological survey; Stochastic chain-binomial model.

Fig. 1

Schematic overview of the flows of individuals in the compartmental model: Following SARS-CoV-2/COVID-19 infection susceptible individuals ($S$) move to an exposed state ($E$) and after a latent period individuals further progress to a pre-symptomatic state ($I_{presym}$) in which they can infect others. Consequently, individuals stay either completely symptom-free ($I_{asym}$) or develop mild symptoms ($I_{mild}$). Asymptomatic individuals will recover over time. Upon having mild symptoms, persons either recover ($R$) or require hospitalization (going from $I_{sev}$ to $I_{hosp}$ or $I_{icu}$) prior to recovery ($R$) or death ($D$).

Fig. 2

Stochastic realizations of the compartmental model based on a thinned MCMC chain from the joint posterior distribution of the model parameters and relying on an ‘asymptomatic’ and ‘symptomatic’ social contact matrix composed of 20% of regular work and transportation contacts, no school contacts and 10% of leisure contacts and contacts related to other activities. Shaded areas represent 95% credible intervals. Reported daily number of hospitalizations and deaths are represented by black circles.

Fig. 3

Stochastic realizations of the compartmental model based on a thinned MCMC chain from the joint posterior distribution of the model parameters and relying on an ‘asymptomatic’ and ‘symptomatic’ social contact matrix composed of 20% of regular work and transportation contacts, no school contacts and 10% of leisure contacts and contacts related to other activities. Number of new hospitalizations (left upper and lower panels) and deaths (right upper and lower panels) are shown for all 10 age groups. Shaded areas represent 95% credible intervals. Reported daily number of hospitalizations and deaths are represented by circles.

Fig. 4

Boxplots of the marginal posterior distributions of the probability of hospitalization by age group.

Fig. 5

Estimated age-dependent seroprevalence of COVID-19 with 95% credible interval on March 30, 2020 (left panel) and April 20, 2020 (right panel). Observed seroprevalences are depicted using red dots with 95% confidence intervals in blue. The confidence interval for the age group $[0,10)$ is wide due to the low number of individuals ($n=36$).

Fig. 6

Estimated time-dependent prevalence of COVID-19 in the different age groups and its weighted average (right panel; black dashed line — right y-axis) based on 5000 stochastic realizations given random draws from the joint posterior distribution of the model parameters with 95% credible intervals (shaded regions).

Fig. 7

Impact of various exit strategies in terms of the number of work- and leisure-related contacts on the number of new hospitalizations in the absence of re-opening of schools.

Fig. 8

Impact of partial re-opening of schools on the number of new hospitalizations.

Fig. 9

Long-term predictions of the impact of various exit strategies on the number of new hospitalizations.

Fig. 10

Predictions of the prevalence in exit scenarios S7–S9 for age group $[0,10)$ (top row), $[30,40)$ (row 2), $[60,70)$ (row 3) and $90+$ (bottom row). Increments in prevalence compared to the prevalence on May 1, 2020 is added on top of the boxplots.

Fig. 11

Stochastic realizations based on the baseline scenario (without change in contact behaviour upon relaxing the stringent lockdown measures) for the number of new hospitalizations (left panel) and the number of new deaths (right panel) together with observed data points used for fitting (black open circles) and for validation (black solid circles).