Benefits of Spectral Property Engineering in Distributed Brillouin Fiber Sensing
- PMID: 33800206
- PMCID: PMC7962463
- DOI: 10.3390/s21051881
Benefits of Spectral Property Engineering in Distributed Brillouin Fiber Sensing
Abstract
As one of the most consolidated distributed fiber sensors based on stimulated Brillouin scattering, the Brillouin optical time-domain analyzer (BOTDA) has been developed for decades. Despite the commercial availability and outstanding progresses which has been achieved, the intrinsic Lorentzian gain spectrum restricts the sensing performance from possible further enhancements and hence limits the field of validity of the technique. In this paper, the novel method of engineering the gain spectral properties of the Brillouin scattering and its application on static and dynamic BOTDA sensors will be reviewed. Such a spectral property engineering has not only provided improvements to BOTDA, but also might open a new way to enhance the performance of all kinds of distributed Brillouin fiber sensors.
Keywords: Brillouin optical time-domain analyzer; distributed fiber sensing; slope-assisted Brillouin optical time-domain analyzer; spectral property engineering; stimulated Brillouin scattering.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
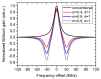



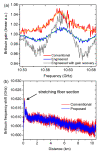










Similar articles
-
Bi-Directional Brillouin Optical Time Domain Analyzer System for Long Range Distributed Sensing.Sensors (Basel). 2016 Dec 16;16(12):2156. doi: 10.3390/s16122156. Sensors (Basel). 2016. PMID: 27999250 Free PMC article.
-
Support vector machine assisted BOTDA utilizing combined Brillouin gain and phase information for enhanced sensing accuracy.Opt Express. 2017 Dec 11;25(25):31210-31220. doi: 10.1364/OE.25.031210. Opt Express. 2017. PMID: 29245798
-
Mitigating the effects of the gain-dependence of the Brillouin line-shape on dynamic BOTDA sensing methods.Opt Express. 2017 Sep 18;25(19):22206-22218. doi: 10.1364/OE.25.022206. Opt Express. 2017. PMID: 29041535
-
Review: distributed time-domain sensors based on Brillouin scattering and FWM enhanced SBS for temperature, strain and acoustic wave detection.Photonix. 2021;2(1):14. doi: 10.1186/s43074-021-00038-w. Epub 2021 Jul 30. Photonix. 2021. PMID: 34841256 Free PMC article. Review.
-
Distributed Dynamic Strain Sensing Based on Brillouin Scattering in Optical Fibers.Sensors (Basel). 2020 Oct 1;20(19):5629. doi: 10.3390/s20195629. Sensors (Basel). 2020. PMID: 33019695 Free PMC article. Review.
Cited by
-
Improving Prediction Accuracy and Extraction Precision of Frequency Shift from Low-SNR Brillouin Gain Spectra in Distributed Structural Health Monitoring.Sensors (Basel). 2022 Mar 31;22(7):2677. doi: 10.3390/s22072677. Sensors (Basel). 2022. PMID: 35408291 Free PMC article.
-
Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes.Sensors (Basel). 2022 Apr 8;22(8):2866. doi: 10.3390/s22082866. Sensors (Basel). 2022. PMID: 35458851 Free PMC article.
References
-
- Kersey A.D., Davis M.A., Patrick H.J., LeBlanc M., Koo K.P., Askins C.G., Putnam M.A., Friebele E.J. Fiber grating sensors. J. Light. Technol. 1997;15:1442–1463. doi: 10.1109/50.618377. - DOI
-
- Galindez-Jamioy C.A., López-Higuera J.M. Brillouin Distributed Fiber Sensors: An Overview and Applications. J. Sens. 2012;2012:204121. doi: 10.1155/2012/204121. - DOI
-
- Feng C., Emad Kadum J., Schneider T. Fiber Optic Sensing—Principle, Measurement and Applications. IntechOpen; London, UK: 2019. The State-of-the-Art of Brillouin Distributed Fiber Sensing. - DOI
-
- Motil A., Bergman A., Tur M. [INVITED] State of the art of Brillouin fiber-optic distributed sensing. Opt. Laser Technol. 2016;78:81–103. doi: 10.1016/j.optlastec.2015.09.013. - DOI
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

