Two-Qubit Local Fisher Information Correlation beyond Entanglement in a Nonlinear Generalized Cavity with an Intrinsic Decoherence

Abstract

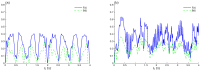
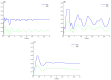
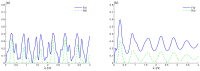
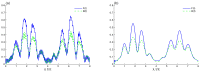
In this paper, we study a Hamiltonian system constituted by two coupled two-level atoms (qubits) interacting with a nonlinear generalized cavity field. The nonclassical two-qubit correlation dynamics are investigated using Bures distance entanglement and local quantum Fisher information under the influences of intrinsic decoherence and qubit-qubit interaction. The effects of the superposition of two identical generalized coherent states and the initial coherent field intensity on the generated two-qubit correlations are investigated. Entanglement of sudden death and sudden birth of the Bures distance entanglement as well as the sudden changes in local Fisher information are observed. We show that the robustness, against decoherence, of the generated two-qubit correlations can be controlled by qubit-qubit coupling and the initial coherent cavity states.

Keywords: SU(2)-algebraic treatment; intrinsic decoherence SU(1,1); nonclassical correlation.

Figure 1

Local quantum Fisher information (LQFI) and Bures distance entanglement (BDE) dynamics of the uncorrelated two-qubit state when the initial cavity field is in the B-GCS ($r=0$) with $k=\frac{1}{2}$ and the initial coherent intensity ${\left|\alpha \right|}^2=16$ in the absence of the intrinsic decoherence. The qubit–qubit coupling effect is shown with different values $J=0$ in (a) and $J=20$$\lambda$ in (b).

Figure 2

LQFI and BDE dynamics when the initial cavity field is in the B-GCS with $k=\frac{1}{2}$ and the initial coherent intensity ${\left|\alpha \right|}^2=16$ in the presence of the intrinsic decoherence effect $\gamma =0.01\lambda$ in (a,b), $\gamma =0.1\lambda$ in (c). The qubit–qubit coupling effect is shown with different values $J=0$ in (a) and $J=20$$\lambda$ in (b).

Figure 3

LQFI and BDE dynamics in the case where the initial cavity field is in the even B-GCS ($r=1$) with the initial coherent intensity ${\left|\alpha \right|}^2=16$ and the intrinsic decoherence is absent. With different values of qubit–qubit coupling, $J=0$ in (a) and $J=20$$\lambda$ in (b).

Figure 4

LQFI and BDE dynamics when the initial cavity field is in the even B-GCS with $k=\frac{1}{2}$ and the initial coherent intensity ${\left|\alpha \right|}^2=16$ in the presence of the intrinsic decoherence effect $\gamma =0.01\lambda$ in (a,b), $\gamma =0.1\lambda$ in (c). The qubit–qubit coupling effect is shown with different values $J=0$ in (a) and $J=20$$\lambda$ in (b).

Figure 5

LQFI and BDE dynamics when the initial cavity field is in the B-GCS with $k=\frac{1}{2}$, small initial coherent intensity ${\left|\alpha \right|}^2=1$, and the qubit–qubit coupling effect is absent. The decoherence effect is shown with different values $\gamma =0.0$ in (a) and $\gamma =0.01$$\lambda$ in (b).

Figure 6

LQFI and BDE dynamics when the initial cavity field is in the B-GCS with $k=\frac{1}{2}$, small initial coherent intensity ${\left|\alpha \right|}^2=1$ in the presence of the qubit–qubit coupling effect $J=20$$\lambda$. The decoherence effect is shown with different values $\gamma =0.0$ in (a) and $\gamma =0.01\lambda$ in (b).