Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Mar 2;21(5):1712.
doi: 10.3390/s21051712.

Real-Time Prognostics of Engineered Systems under Time Varying External Conditions Based on the COX PHM and VARX Hybrid Approach

Hongmin Zhu  1
Affiliations

Real-Time Prognostics of Engineered Systems under Time Varying External Conditions Based on the COX PHM and VARX Hybrid Approach

Hongmin Zhu. Sensors (Basel). .

Abstract

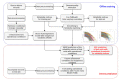
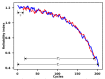
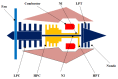
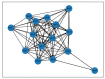
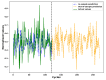
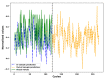
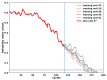
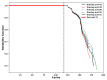
In spite of the development of the Prognostics and Health Management (PHM) during past decades, the reliability prognostics of engineered systems under time-varying external conditions still remains a challenge in such a field. When considering the challenge mentioned above, a hybrid method for predicting the reliability index and the Remaining Useful Life (RUL) of engineered systems under time-varying external conditions is proposed in this paper. The proposed method is competent in reflecting the influence of time-varying external conditions on the degradation behaviour of engineered systems. Based on a subset of the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS) dataset as case studies, the Cox Proportional Hazards Model (Cox PHM) with time-varying covariates is utilised to generate the reliability indices of individual turbofan units. Afterwards, a Vector Autoregressive model with Exogenous variables (VARX) combined with pairwise Conditional Granger Causality (CGC) tests for sensor selections is defined to model the time-varying influence of sensor signals on the reliability indices of different units that have been previously generated by the Cox PHM with time-varying covariates. During the reliability prediction, the Fourier Grey Model (FGM) is employed with the time series models for long-term forecasting of the external conditions. The results show that the method that is proposed in this paper is competent for the RUL prediction as compared with baseline approaches.

Keywords: Conditional Granger Causality (CGC); Cox proportional hazards model (PHM); Fourier Grey model (FGM); Vector Autoregressive model with exogenous variables (VARX); prognostics; time-varying covariates.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Schematic sketch of the algorithm proposed in this research.
Figure 2
Figure 2
Illustration of the similarity matching process of relaibility indices.
Figure 3
Figure 3
Inner structure of the turbofan employed in the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS) data sets [78].
Figure 4
Figure 4
Statistical causal graphs of units in FD001 training set generated by the CGC test.
Figure 5
Figure 5
Similarity matching between the incomplete reliability index of the 37th unit in the test set and its five most similar reliability indices of the units in the run-to-failure training set.The similarity decreases with the figure order. (a) Incomplete reliability index of the 37th unit in the test set matched with the complete reliability index of the 45th unit in the training set. (b) Incomplete reliability index of the 37th unit in the test set matched with the complete reliability index of the 28th unit in the training set. (c) Incomplete reliability index of the 37th unit in the test set matched with the complete reliability index of the 98th unit in the training set. (d) Incomplete reliability index of the 37th unit in the test set matched with the complete reliability index of the 93rd unit in the training set. (e) Incomplete reliability index of the 37th unit in the test set matched with the complete reliability index of the 61st unit in the training set.
Figure 6
Figure 6
Box plot of the RMSE and the NRMSE of the in-sample fitting of the VARX models based on training set units.
Figure 7
Figure 7
In-sample fitting of the first operational conditions of the unit 37 in FD001 test sets based on the FGM(1, 1) and ARIMA/ARMA calibration.
Figure 8
Figure 8
In-sample fitting of the second operational conditions of the unit 37 in FD001 test sets based on the FGM(1, 1) and ARIMA/ARMA calibration.
Figure 9
Figure 9
Prediction of the first operational conditions of the unit 37 in FD001 test sets based on the FGM(1, 1) and ARIMA/ARMA calibration.
Figure 10
Figure 10
Prediction of the second operational conditions of the unit 37 in FD001 test sets based on the FGM(1, 1) and ARIMA/ARMA calibration.
Figure 11
Figure 11
Predictions of the incomplete reliability index of the test set unit 37th considering its five most similar reliability indices of the training set units. The online prediction of the reliability index for the unit 37th in the test set is updated by future values of the external operational conditions which are predicted by means of the FGM model.
Figure 12
Figure 12
Predictions of the reliability function of the test set unit 37th considering its five most similar reliability indices of the training set units.
Figure 13
Figure 13
Comparision between the actual RULs and their prediction values.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Frankel E.G. Systems Reliability and Risk Analysis. 1st ed. Springer Science & Business Media; Dordrecht, The Netherlands: 1984. Basic Concepts of Reliability; pp. 15–16.
    1. Høyland A., Rausand M. System Reliability Theory: Models and Statistical Methods. 1st ed. John Wiley & Sons; Hoboken, NJ, USA: 1994. Basic Concepts; pp. 5–6.
    1. Javed K., Gouriveau R., Zerhouni N. State of the art and taxonomy of prognostics approaches, trends of prognostics applications and open issues towards maturity at different technology readiness levels. Mech. Syst. Signal Process. 2017;94:214–236. doi: 10.1016/j.ymssp.2017.01.050. - DOI
    1. ISO . Condition Monitoring and Diagnostics of Machines—Prognostics. ISO; Geneva, Switzerland: 2015. BS ISO 13381-1:2015.
    1. Sankararaman S., Daigle M.J., Goebel K. Uncertainty quantification in remaining useful life prediction using first-order reliability methods. IEEE Trans. Reliab. 2014;63:603–619. doi: 10.1109/TR.2014.2313801. - DOI

LinkOut - more resources