Simplitigs as an efficient and scalable representation of de Bruijn graphs
- PMID: 33823902
- PMCID: PMC8025321
- DOI: 10.1186/s13059-021-02297-z
Simplitigs as an efficient and scalable representation of de Bruijn graphs
Abstract
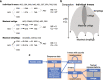
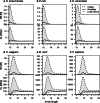
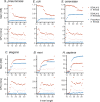
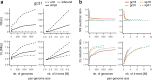
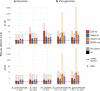
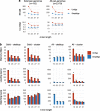
de Bruijn graphs play an essential role in bioinformatics, yet they lack a universal scalable representation. Here, we introduce simplitigs as a compact, efficient, and scalable representation, and ProphAsm, a fast algorithm for their computation. For the example of assemblies of model organisms and two bacterial pan-genomes, we compare simplitigs to unitigs, the best existing representation, and demonstrate that simplitigs provide a substantial improvement in the cumulative sequence length and their number. When combined with the commonly used Burrows-Wheeler Transform index, simplitigs reduce memory, and index loading and query times, as demonstrated with large-scale examples of GenBank bacterial pan-genomes.
Keywords: Data compression; Indexing; Pan-genomes; Scalability; Sequence analysis; Simplitigs; Storage; de Bruijn graph representation; de Bruijn graphs; k-mers.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures

References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

