Optimized permutation testing for information theoretic measures of multi-gene interactions

Abstract

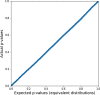
Background: Permutation testing is often considered the "gold standard" for multi-test significance analysis, as it is an exact test requiring few assumptions about the distribution being computed. However, it can be computationally very expensive, particularly in its naive form in which the full analysis pipeline is re-run after permuting the phenotype labels. This can become intractable in multi-locus genome-wide association studies (GWAS), in which the number of potential interactions to be tested is combinatorially large.

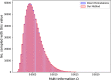
Results: In this paper, we develop an approach for permutation testing in multi-locus GWAS, specifically focusing on SNP-SNP-phenotype interactions using multivariable measures that can be computed from frequency count tables, such as those based in Information Theory. We find that the computational bottleneck in this process is the construction of the count tables themselves, and that this step can be eliminated at each iteration of the permutation testing by transforming the count tables directly. This leads to a speed-up by a factor of over 10³ for a typical permutation test compared to the naive approach. Additionally, this approach is insensitive to the number of samples making it suitable for datasets with large number of samples.

Conclusions: The proliferation of large-scale datasets with genotype data for hundreds of thousands of individuals enables new and more powerful approaches for the detection of multi-locus genotype-phenotype interactions. Our approach significantly improves the computational tractability of permutation testing for these studies. Moreover, our approach is insensitive to the large number of samples in these modern datasets. The code for performing these computations and replicating the figures in this paper is freely available at https://github.com/kunert/permute-counts .

Keywords: Information theory; Multi-locus GWAS; Multivariable interactions; Permutation testing.

Fig. 1

a Computation time as a function of the number of permutations $N_p$, for a synthetic dataset with a fixed number of individuals $n=10,000$ and 100 k SNPs. Both direct permutations (in blue) and our method (in orange) are $\mathcal{O}(N_p)$ (note that the horizontal axis is logarithmic, and the best fit lines plotted here are indeed linear). Our method is faster by a factor of over ${10}^3$ per permutation. b Computation time as a function of the number of individuals n, for a synthetic dataset with a fixed number of permutations $N_p=20$ and 100 k SNPs. Direct permutation is $\mathcal{O}(n)$ but our approach is $\mathcal{O}(1)$ (i.e. computation time does not depend on the number of samples for this approach)

Fig. 2

Using the simulated data described in Sect. , we generated 1,000,000 permuted count tables using both the naive method of directly permuting the phenotype labels and using our approach. The distributions of the count table elements $c_{ij0}^{\ast }$ are plotted here, with the direct permutation result shown in blue and our method shown in red. The plot consists almost entirely of the purple overlapping region, as there is almost no visible difference between the distributions

Fig. 3

The permuted count tables from Sect.  can be used to calculate the joint entropies, from which we can calculate any information theoretic measure which is a function of the entropies. Here we calculate the multi-information $\mathrm{\Omega }$ using both the count tables generated by direct permutations and by our method, with the resulting distributions being nearly identical

Fig. 4

Quantile–quantile plot of p values from Epps–Singleton tests comparing the two distributions. The null hypothesis is that the two distributions are identical. Under the null hypothesis, the p value is uniformly distributed and we would expect the Q–Q plot to be linear along the diagonal, which is what we observe. The count table distributions generated from each method are indistinguishable via this test