Neuromechanical wave resonance in jellyfish swimming

Abstract

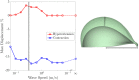
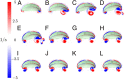
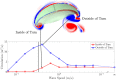
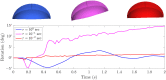
For organisms to have robust locomotion, their neuromuscular organization must adapt to constantly changing environments. In jellyfish, swimming robustness emerges when marginal pacemakers fire action potentials throughout the bell's motor nerve net, which signals the musculature to contract. The speed of the muscle activation wave is dictated by the passage times of the action potentials. However, passive elastic material properties also influence the emergent kinematics, with time scales independent of neuromuscular organization. In this multimodal study, we examine the interplay between these two time scales during turning. A three-dimensional computational fluid-structure interaction model of a jellyfish was developed to determine the resulting emergent kinematics, using bidirectional muscular activation waves to actuate the bell rim. Activation wave speeds near the material wave speed yielded successful turns, with a 76-fold difference in turning rate between the best and worst performers. Hyperextension of the margin occurred only at activation wave speeds near the material wave speed, suggesting resonance. This hyperextension resulted in a 34-fold asymmetry in the circulation of the vortex ring between the inside and outside of the turn. Experimental recording of the activation speed confirmed that jellyfish actuate within this range, and flow visualization using particle image velocimetry validated the corresponding fluid dynamics of the numerical model. This suggests that neuromechanical wave resonance plays an important role in the robustness of an organism's locomotory system and presents an undiscovered constraint on the evolution of flexible organisms. Understanding these dynamics is essential for developing actuators in soft body robotics and bioengineered pumps.

Keywords: fluid–structure interaction; jellyfish; maneuverability; neuromechanics; propulsion.

Fig. 1.

(A–F) DPIV frames of the vorticity of an Aurelia sp. executing a turn. (G–L) Snapshots of the model bell ($\nu ={\nu }_{ref}$, $\tau =10^{-0.4}$ s) and the out-of-plane vorticity generated by a second wave of active tension at times 2.0 s (G), 2.2 s (H), 2.375 s (I), 2.5 s (J), 2.75 s (K), and 3.0 s (L). The bell color indicates the instantaneous strength of contraction, in which dark green indicates the presence of tension and white is the absence of tension.

Fig. 2.

Half-plane plot lots of the bell model’s mesh at time 0.75 s (A), along with isocontours of the vorticity magnitude (${\mathrm{s}}^{-1}$) (B), $y$ component of vorticity (${\mathrm{s}}^{-1}$) (C), pressure (N/${\mathrm{m}}^2$) (D), and the vertical velocity (m/s) (E). The starting and stopping vortex rings are labeled 1 and 2, respectively, in B and C. The isocontours are symmetric across the $xz$ plane.

Fig. 3.

(Left) Plot of the percentage of hyperextension (red) and contraction (blue) of the bell margin on the outside of the turn for differing activation wave speeds. Note that the bell margin only hyperextends for activation wave speeds near the material wave speed (black). (Right) A diagram displaying how the hyperextension of the bell margin is measured.

Fig. 4.

Plots of the out-of-plane vorticity 0.5 s after the passage of the activation wave for different runs where $c_a=$ $r\cdot \pi /10^{0.0}$ m/s (A), $r\cdot \pi /10^{-0.2}$ m/s (B), $r\cdot \pi /10^{-0.4}$ m/s (C), $r\cdot \pi /10^{-0.6}$ m/s (D), $r\cdot \pi /10^{-0.8}$ m/s (E), $r\cdot \pi /10^{-1.0}$ (F), $r\cdot \pi /10^{-1.2}$ m/s (G), $r\cdot \pi /10^{-1.4}$ m/s (H), $10^{-1.6}$ m/s (I), $r\cdot \pi /10^{-1.8}$ m/s (J), $r\cdot \pi /10^{-2.0}$ m/s (K), and 0.0 m/s (L). The bell is initially at rest in quiescent flow.

Fig. 5.

Plot comparing the circulation of the inside (red) and outside (blue) of the turn 0.5 s after the passage of the wave of muscular activation for various activation wave speeds, with the material wave speed, $c_r$, noted in black. We observe that the circulation generated on the outside of the turn increases as the activation wave speed approaches the material wave speed, peaking at a speed slightly higher than that of the material wave speed. The circulation found on the inside of the turn is initially minimal, but then grows for $c_a\ge r\cdot \pi /r\cdot \pi 10^{-0.8}$ before plateauing. At faster activation wave speeds, the circulation between the inside and outside of the turn begin to converge, as would be expected for a uniform activation of the bell.

Fig. 6.

Plot comparing the turn angle along the central axis of the bell ($\nu ={\nu }_{\mathrm{r}\mathrm{e}\mathrm{f}}$) for three wave speeds, $c_a=r\cdot \pi /10^0$, $r\cdot \pi /10^{-1}$, and $r\cdot \pi /10^{-2}$ m/s. We note that the activation wave speed corresponding to the closest to the material wave speed, $c_a=r\cdot \pi /10^{-1}$ m/s, yields a significant turn. We also note that the bell in this case continues to turn long after the activation wave due to the vortex dynamics shown in Fig. 4.

Fig. 7.

Plot comparing the resulting turn angle of three bells with $\nu =1/4{\nu }_{ref}$ (dashed), ${\nu }_{ref}$ (solid), and $4{\nu }_{ref}$ (dotted), at 2 s for differing activation wave speeds. We note that the peak turn angle is near the associated material wave speed (plotted in black). This suggests that this turning mechanism is strongly dependent on the interaction between the material properties of the bell and the speed of neuromuscular activation. Shaded in green is the range of speeds observed in A. aurita, with the solid green line representing the mean wave speed recorded.

Fig. 8.

Plot of the turn angle relative to the center axis of the bell in subsequent 2-s activation cycles for the activation wave speed near the material wave speed, $c_a=r\cdot \pi /10^{-0.6}$ m/s. We note that the bell continues to consistently turn with each application of the activation wave, which suggests a robust a turning mechanism.

Fig. 9.

Experiments to measure jellyfish muscle contractile speeds. (A) To calculate experimental muscle wave speeds, muscle contractions of jellyfish were recorded using movies taken at 60 fps. (A, Left) A schematic of the jellyfish bell, with labels for the oral arms, rhopalia, muscle ring, electrode with arrows showing the bidirectional muscle wave propagation, and injected tags. (A, Right) A representative frame for one animal (diameter of 8.5 cm). The raw image includes reflections of light from the transparent mesoglea and black plate. The jellyfish (bell outlined in yellow) was placed subumbrellar surface upward on a black dish in the absence of water. An electrode (circled in blue) was embedded into the tissue, with a red light-emitting diode shown for visual confirmation of the electrical signal. Red tags were injected into the marginal tissue (two tags circled in red). The circled tags, labeled 1 and 2, were tracked to obtain displacement curves, as shown in one example displacement curve in B, in which one animal was driven at 0.25 Hz. The time delay between the two tags was used to calculate the muscle wave-propagation speed. Additional displacements are illustrated in SI Appendix, Fig. S2.