Modeling programmable drug delivery in bioelectronics with electrochemical actuation

Abstract

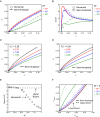
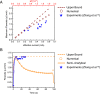
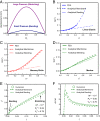
Drug delivery systems featuring electrochemical actuation represent an emerging class of biomedical technology with programmable volume/flowrate capabilities for localized delivery. Recent work establishes applications in neuroscience experiments involving small animals in the context of pharmacological response. However, for programmable delivery, the available flowrate control and delivery time models fail to consider key variables of the drug delivery system--microfluidic resistance and membrane stiffness. Here we establish an analytical model that accounts for the missing variables and provides a scalable understanding of each variable influence in the physics of delivery process (i.e., maximum flowrate, delivery time). This analytical model accounts for the key parameters--initial environmental pressure, initial volume, microfluidic resistance, flexible membrane, current, and temperature--to control the delivery and bypasses numerical simulations allowing faster system optimization for different in vivo experiments. We show that the delivery process is controlled by three nondimensional parameters, and the volume/flowrate results from the proposed analytical model agree with the numerical results and experiments. These results have relevance to the many emerging applications of programmable delivery in clinical studies within the neuroscience and broader biomedical communities.

Keywords: analytical model; drug delivery; electrochemical actuation; flexible membrane; mechanics.

Fig. 1.

Schematic diagram of the electrochemical micropump system. (A) Before, (B) during, and (C) after the drug delivery process highlighting the relevant volume, pressure, and microchannel parameters in the drug delivery process.

Fig. 2.

Drug delivery models and scaling results. (A) Numerical and semianalytical model results for normalized drug volume delivery and (B) normalized flowrate over normalized time for different $M^{\ast }$. Normalized drug volume delivery for different (C) initial volume $V_0^{\ast }$ and (D) initial environmental pressure $P_0^{\ast }$. (E) Maximum normalized flowrate and the upper bound as a function of $M^{\ast }$ in the numerical model. (F) Critical normalized time to deliver normalized drug volume for different $M^{\ast }$; the lower bound corresponds to $M^{\ast }=0$. In the semianalytical model, the term $f\left(V\right)$ is obtained from FEA.

Fig. 3.

Drug delivery experiments and modeling. (A) Maximum flowrate as a function of effective current for the upper-bound solution (wine dashed line), numerical (wine circles), and experimental data in Zhang et al. (15) (blue stars) for a system with microchannel cross-section 30 μm × 30 μm. (B) Flowrate as a function of time models for the upper-bound solution (orange dashed line), numerical (orange circles), semianalytical model (orange continuous line), and experimental data in Zhang et al. (16) (blue stars) for a system with microchannel cross-section 60 μm × 60 μm.

Fig. 4.

Flexible membrane deformation mechanics. (A) FEA results of membrane displacement (bending-dominated and stretching-dominated) as a function of the membrane radius. (B) Nondimensional function $G\left(V^{\ast }\right)$ as a function of $V^{\ast }$between FEA (solid line), membrane solution (dashed line), and bending solution (dotted line) for a linear elastic material, (C) Mooney Rivlin hyperelastic material, and (D) Marlow hyperelastic material. (E) Nondimensional volume and (F) nondimensional flowrate as a function of nondimensional time for the Marlow hyperelastic material in (D) with different $G\left(V^{\ast }\right)$ solutions for the baseline nondimensional parameters. The analytical model uses the analytic expression of $f\left(V\right)$ determined for the different material models.