Flexible modulation of sequence generation in the entorhinal-hippocampal system
- PMID: 33846626
- PMCID: PMC7610914
- DOI: 10.1038/s41593-021-00831-7
Flexible modulation of sequence generation in the entorhinal-hippocampal system
Abstract
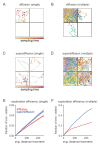
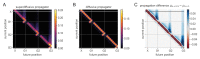
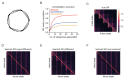
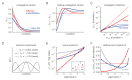
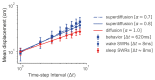
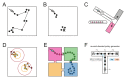
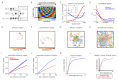
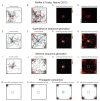
Exploration, consolidation and planning depend on the generation of sequential state representations. However, these algorithms require disparate forms of sampling dynamics for optimal performance. We theorize how the brain should adapt internally generated sequences for particular cognitive functions and propose a neural mechanism by which this may be accomplished within the entorhinal-hippocampal circuit. Specifically, we demonstrate that the systematic modulation along the medial entorhinal cortex dorsoventral axis of grid population input into the hippocampus facilitates a flexible generative process that can interpolate between qualitatively distinct regimes of sequential hippocampal reactivations. By relating the emergent hippocampal activity patterns drawn from our model to empirical data, we explain and reconcile a diversity of recently observed, but apparently unrelated, phenomena such as generative cycling, diffusive hippocampal reactivations and jumping trajectory events.
Conflict of interest statement
Daniel McNamee and Samuel Gershman declare no competing interests. Kimberly Stachenfeld and Matthew Botvinick are employed by Google DeepMind.
Figures





References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

