Multiscale modeling of glioma pseudopalisades: contributions from the tumor microenvironment
- PMID: 33846838
- PMCID: PMC8041715
- DOI: 10.1007/s00285-021-01599-x
Multiscale modeling of glioma pseudopalisades: contributions from the tumor microenvironment
Abstract
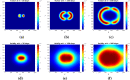
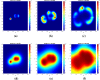
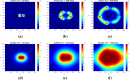
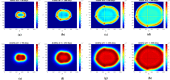
Gliomas are primary brain tumors with a high invasive potential and infiltrative spread. Among them, glioblastoma multiforme (GBM) exhibits microvascular hyperplasia and pronounced necrosis triggered by hypoxia. Histological samples showing garland-like hypercellular structures (so-called pseudopalisades) centered around the occlusion site of a capillary are typical for GBM and hint on poor prognosis of patient survival. We propose a multiscale modeling approach in the kinetic theory of active particles framework and deduce by an upscaling process a reaction-diffusion model with repellent pH-taxis. We prove existence of a unique global bounded classical solution for a version of the obtained macroscopic system and investigate the asymptotic behavior of the solution. Moreover, we study two different types of scaling and compare the behavior of the obtained macroscopic PDEs by way of simulations. These show that patterns (not necessarily of Turing type), including pseudopalisades, can be formed for some parameter ranges, in accordance with the tumor grade. This is true when the PDEs are obtained via parabolic scaling (undirected tissue), while no such patterns are observed for the PDEs arising by a hyperbolic limit (directed tissue). This suggests that brain tissue might be undirected - at least as far as glioma migration is concerned. We also investigate two different ways of including cell level descriptions of response to hypoxia and the way they are related .
Keywords: Directed/undirected tissue; Glioblastoma; Global existence; Hypoxia-induced tumor behavior; Kinetic transport equations; Long time behavior; Multiscale modeling; Pseudopalisade patterns; Reaction-diffusion-taxis equations; Uniqueness; Upscaling.
Figures



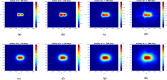
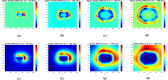

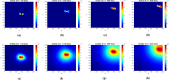
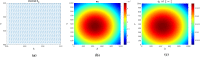

Similar articles
-
Data driven modeling of pseudopalisade pattern formation.J Math Biol. 2023 Jun 10;87(1):4. doi: 10.1007/s00285-023-01933-5. J Math Biol. 2023. PMID: 37300719
-
Pseudopalisades in glioblastoma are hypoxic, express extracellular matrix proteases, and are formed by an actively migrating cell population.Cancer Res. 2004 Feb 1;64(3):920-7. doi: 10.1158/0008-5472.can-03-2073. Cancer Res. 2004. PMID: 14871821
-
Hypoxic cell waves around necrotic cores in glioblastoma: a biomathematical model and its therapeutic implications.Bull Math Biol. 2012 Dec;74(12):2875-96. doi: 10.1007/s11538-012-9786-1. Epub 2012 Nov 14. Bull Math Biol. 2012. PMID: 23151957 Free PMC article.
-
Overcoming the blood-brain tumor barrier for effective glioblastoma treatment.Drug Resist Updat. 2015 Mar;19:1-12. doi: 10.1016/j.drup.2015.02.002. Epub 2015 Mar 6. Drug Resist Updat. 2015. PMID: 25791797 Review.
-
Vaso-occlusive and prothrombotic mechanisms associated with tumor hypoxia, necrosis, and accelerated growth in glioblastoma.Lab Invest. 2004 Apr;84(4):397-405. doi: 10.1038/labinvest.3700070. Lab Invest. 2004. PMID: 14990981 Review.
Cited by
-
Modelling the Tumour Microenvironment, but What Exactly Do We Mean by "Model"?Cancers (Basel). 2023 Jul 26;15(15):3796. doi: 10.3390/cancers15153796. Cancers (Basel). 2023. PMID: 37568612 Free PMC article. Review.
References
-
- Bartel P, Ludwig FT, Schwab A, Stock C. pH-taxis: directional tumor cell migration along pH-gradients. Acta Physiologica. 2012;204(Suppl. 689):113.
-
- Bellomo N. Modeling complex living systems. Boston: Birkhäuser; 2008.
-
- Böttger K, Hatzikirou H, Chauviere A, Deutsch A. Investigation of the migration/proliferation dichotomy and its impact on avascular glioma invasion. Math Model Nat Phenom. 2012;7:105–135.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

